
【题目】已知函数![]() ,
,![]() .
.
(I)讨论![]() 的单调性;
的单调性;
(II)若![]() 恒成立,证明:当
恒成立,证明:当![]() 时,
时,![]() .
.
(III)在(II)的条件下,证明:![]() .
.
【答案】I.见解析;Ⅱ.见解析;III 见解析.
【解析】
I:对函数求导,分类讨论导函数的正负,进而得到单调性;Ⅱ:通过分类讨论可得到a=1,根据![]() ,得到:
,得到:![]() ,进而得到结果; III:通过讨论函数的单调性得到
,进而得到结果; III:通过讨论函数的单调性得到![]() ,进而得到:
,进而得到:![]() ,由Ⅱ知
,由Ⅱ知![]() 两式相乘得到结果.
两式相乘得到结果.
I.![]()
若![]() ,f(x)在
,f(x)在![]() 上递增;
上递增;
若a>0,当![]() 时,
时,![]() ,f(x)单调递增;
,f(x)单调递增;
当![]() 时,
时,![]() 单调递减。
单调递减。
Ⅱ.由I知,若a≤0,f(x)在(0,+![]() )上递增,又f(l)=0,故f(x)≤0不恒成立
)上递增,又f(l)=0,故f(x)≤0不恒成立
若a>1,当![]() 时,f(x)递减,f(x)>f(1)=0,不合题意。
时,f(x)递减,f(x)>f(1)=0,不合题意。
若0<a<1,当![]() 时,f(x)递增,f(x)>f(l)=0.不合题意。
时,f(x)递增,f(x)>f(l)=0.不合题意。
若a=1.f(x)在(0,1)上递增.在(1,+![]() )上递减,f(x)≤f(1)=0,合题意。
)上递减,f(x)≤f(1)=0,合题意。
故a=1,且![]() (当且仅当x=1时取 “=”)
(当且仅当x=1时取 “=”)
当0<x1<x2时,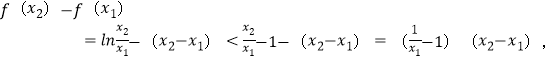
所以![]()
III.![]()
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,g(x)单调递减。
,g(x)单调递减。
![]()
![]() ①
①
由(Ⅱ)知![]() (当且仅当x=1时取 “=”)........... ②
(当且仅当x=1时取 “=”)........... ②
两个不等式的等号不能同时取到,故得到:
①![]() ②得
②得![]()
即![]() ,
,
![]()


科目:高中数学 来源: 题型:
【题目】我国2019年新年贺岁大片《流浪地球》自上映以来引发了社会的广泛关注,受到了观众的普遍好评.假设男性观众认为《流浪地球》好看的概率为![]() ,女性观众认为《流浪地球》好看的概率为
,女性观众认为《流浪地球》好看的概率为![]() .某机构就《流浪地球》是否好看的问题随机采访了4名观众(其中2男2女).
.某机构就《流浪地球》是否好看的问题随机采访了4名观众(其中2男2女).
(1)求这4名观众中女性认为好看的人数比男性认为好看的人数多的概率;
(2)设![]() 表示这4名观众中认为《流浪地球》好看的人数,求
表示这4名观众中认为《流浪地球》好看的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
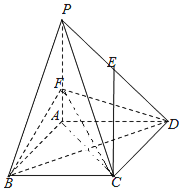
【题目】在四棱锥![]() 中,底面ABCD是边长为6的菱形,且
中,底面ABCD是边长为6的菱形,且![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,F是棱PA上的一个动点,E为PD的中点.
,F是棱PA上的一个动点,E为PD的中点.
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() .
.
![]() Ⅱ
Ⅱ![]() 若
若![]() .
.
![]() 求PC与平面BDF所成角的正弦值;
求PC与平面BDF所成角的正弦值;
![]() 侧面PAD内是否存在过点E的一条直线,使得该直线上任一点M与C的连线,都满足
侧面PAD内是否存在过点E的一条直线,使得该直线上任一点M与C的连线,都满足![]() 平面BDF,若存在,求出此直线被直线PA、PD所截线段的长度,若不存在,请明理由.
平面BDF,若存在,求出此直线被直线PA、PD所截线段的长度,若不存在,请明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起,得到如图2所示的四棱锥D1—ABCE,其中平面D1AE⊥平面ABCE.
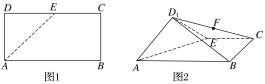
(1)证明:BE⊥平面D1AE;
(2)设F为CD1的中点,在线段AB上是否存在一点M,使得MF∥平面D1AE,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 为集合U的n个非空子集,这n个集合满足:①从中任取m个集合都有
为集合U的n个非空子集,这n个集合满足:①从中任取m个集合都有![]()
![]()
![]() 成立;②从中任取
成立;②从中任取![]() 个集合都有
个集合都有![]()
![]() 成立.
成立.
(Ⅰ)若![]() ,
, ![]() ,
, ![]() ,写出满足题意的一组集合
,写出满足题意的一组集合![]() ;
;
(Ⅱ)若![]() ,
, ![]() ,写出满足题意的一组集合
,写出满足题意的一组集合![]() 以及集合
以及集合![]() ;
;
(Ⅲ) 若![]() ,
, ![]() ,求集合
,求集合![]() 中的元素个数的最小值.
中的元素个数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
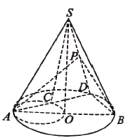
【题目】如图,![]() 是圆锥
是圆锥![]() 的底面
的底面![]() 的直径,
的直径,![]() 是圆
是圆![]() 上异于
上异于![]() 的任意一点,以
的任意一点,以![]() 为直径的圆与
为直径的圆与![]() 的另一个交点为
的另一个交点为![]() 为
为![]() 的中点.现给出以下结论:
的中点.现给出以下结论:
①![]() 为直角三角形
为直角三角形
②平面![]() 平面
平面![]()
③平面![]() 必与圆锥
必与圆锥![]() 的某条母线平行
的某条母线平行
其中正确结论的个数是
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣2y+1=0和抛物线E:y2=2px(p>0),圆C与抛物线E的准线交于M、N两点,△MNF的面积为p,其中F是E的焦点.
(1)求抛物线E的方程;
(2)不过原点O的动直线l交该抛物线于A,B两点,且满足OA⊥OB,设点Q为圆C上任意一动点,求当动点Q到直线l的距离最大时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的方程为
中,曲线C的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线C的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 轴和y轴分别交于A,B两点,P为曲线C上的动点,求△PAB面积的最大值.
轴和y轴分别交于A,B两点,P为曲线C上的动点,求△PAB面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com