已知函数
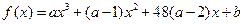
的图象关于原点成中心对称,试判断
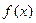
在区间
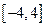
上的单调性,并证明你的结论.
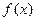
在[-4,4]上是单调递减函数
∵函数
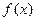
的图象关于原点成中心对称,
则
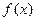
是奇函数,,所以
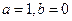
,于是
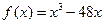
,
∴
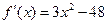
,∴当
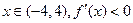
,
又∵函数
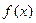
在
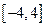
上连续,
所以
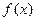
在[-4,4]上是单调递减函数.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
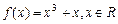
.
(I)指出
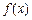
在定义域
R上的奇偶性与单调性(只须写出结论,无须证明);
(II)若
a、
b、
c∈
R,且
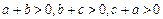
,试证明:
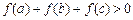
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设函数
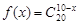
,集合
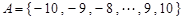
,判断
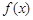
在
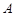
上的奇偶性为( )
| A.偶函数 | B.奇函数 | C.非奇非偶函数 | D.既是奇函数又是偶函数 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数
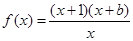
的图象关于原点对称,则
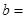
________________.

查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
判断下列函数的奇偶性.
(1)f(x)=
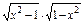
;
(2)f(x)=log
2(x+
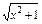
) (x∈R);
(3)f(x)=lg|x-2|.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分12分)已知函数
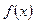
为定义在R上的奇函数,且当
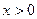
时,
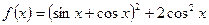
,
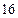
(1) 求
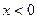
时
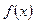
的表达式;
(2) 若关于
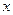
的方程
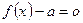
有解,求实数
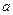
的范围。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设偶函数f(x)满足f(x)=2
x-4 (x
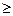
0),则
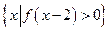
="( " )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设
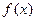
是定义在R上的以3为周期的奇函数,若
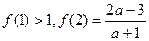
,则实数
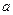
的取值范围是
。
查看答案和解析>>

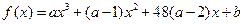 的图象关于原点成中心对称,试判断
的图象关于原点成中心对称,试判断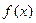 在区间
在区间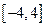 上的单调性,并证明你的结论.
上的单调性,并证明你的结论. 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案