
分析 根据定义在[0,+∞)上的函数f(x)满足f(x)=2f(x+2),可得f(x+2)=$\frac{1}{2}$f(x),从而f(x+2n)=$\frac{1}{{2}^{n}}$f(x),利用当x∈[0,2)时,f(x)=-2x2+4x,可求(x)在[2n-2,2n)上的解析式,从而可得f(x)在[2n-2,2n)上的最大值为an,进而利用等比数列的求和公式,即可求得{an}的前n项和.
解答 解:∵定义在[0,+∞)上的函数f(x)满足f(x)=2f(x+2),
∴f(x+2)=$\frac{1}{2}$f(x),
∴f(x+4)=$\frac{1}{2}$f(x+2)=$\frac{1}{4}$f(x),
f(x+6)=$\frac{1}{2}$f(x+4)=$\frac{1}{8}$f(x),
…
f(x+2n)=$\frac{1}{{2}^{n}}$f(x)
设x∈[2n-2,2n),则x-(2n-2)∈[0,2)
∵当x∈[0,2)时,f(x)=-2x2+4x.
∴f[x-(2n-2)]=-2[(x-(2n-2)]2+4[x-(2n-2)].
∴$\frac{1}{{2}^{1-n}}$f(x)=-2(x-2n+1)2+2
∴f(x)=21-n[-2(x-2n+1)2+2],x∈[2n-2,2n),
∴x=2n-1时,f(x)的最大值为22-n
∴an=22-n
∴{an}表示以2为首项,$\frac{1}{2}$为公比的等比数列
∴{an}的前n项和为Sn=$\frac{2[1-(\frac{1}{2})^{n}]}{1-\frac{1}{2}}$=4-$\frac{1}{{2}^{n-2}}$.
故答案为:4-$\frac{1}{{2}^{n-2}}$.
点评 本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意函数性质、等比数列的性质的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题

| A. | $1+\sqrt{5}$ | B. | $2+\sqrt{5}$ | C. | $1+2\sqrt{5}$ | D. | $2+2\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $3\sqrt{2}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
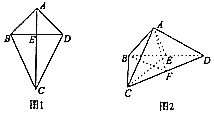 如图1,四边形ABCD中AC⊥BD,CE=2AE=2BE=2DE=2,将四边形ABCD沿着BD折叠,得到图2所示的三棱锥A-BCD,其中AB⊥CD.
如图1,四边形ABCD中AC⊥BD,CE=2AE=2BE=2DE=2,将四边形ABCD沿着BD折叠,得到图2所示的三棱锥A-BCD,其中AB⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com