
ЁОЬтФПЁПЫцзХвЦЖЏЛЅСЊЭјЕФПьЫйЗЂеЙЃЌЛљгкЛЅСЊЭјЕФЙВЯэЕЅГЕгІдЫЖјЩњ.ФГЙВЯэЕЅГЕдЫгЊЙЋЫО![]() ЮЊНјвЛВНРЉДѓЪаГЁЃЌЙЋЫОФтдйВЩЙКвЛХњЕЅГЕ.ЯжгаВЩЙКГЩБОЗжБ№ЮЊ
ЮЊНјвЛВНРЉДѓЪаГЁЃЌЙЋЫОФтдйВЩЙКвЛХњЕЅГЕ.ЯжгаВЩЙКГЩБОЗжБ№ЮЊ![]() дЊ/СОКЭ
дЊ/СОКЭ![]() дЊ/СОЕФ
дЊ/СОЕФ![]() ЁЂ
ЁЂ![]() СНПюГЕаЭПЩЙЉбЁдёЃЌАДЙцЖЈУПСОЕЅГЕзюЖрЪЙгУ
СНПюГЕаЭПЩЙЉбЁдёЃЌАДЙцЖЈУПСОЕЅГЕзюЖрЪЙгУ![]() ФъЃЌЕЋгЩгкЖржждвђЃЈШчЦяааЦЕТЪЕШЃЉЛсЕМжТГЕСОБЈЗЯФъЯоИїВЛЯрЭЌ.ПМТЧЕНЙЋЫОдЫгЊЕФОМУаЇвцЃЌИУЙЋЫООіЖЈЯШЖдСНПюГЕаЭЕФЕЅГЕИї
ФъЃЌЕЋгЩгкЖржждвђЃЈШчЦяааЦЕТЪЕШЃЉЛсЕМжТГЕСОБЈЗЯФъЯоИїВЛЯрЭЌ.ПМТЧЕНЙЋЫОдЫгЊЕФОМУаЇвцЃЌИУЙЋЫООіЖЈЯШЖдСНПюГЕаЭЕФЕЅГЕИї![]() СОНјааПЦбЇФЃФтВтЪдЃЌЕУЕНСНПюЕЅГЕЪЙгУЪйУќЦЕЪ§БэМћЯТБэ.
СОНјааПЦбЇФЃФтВтЪдЃЌЕУЕНСНПюЕЅГЕЪЙгУЪйУќЦЕЪ§БэМћЯТБэ.

ОВтЫуЃЌЦНОљУПСОЕЅГЕУПФъПЩвдДјРДЪеШы![]() дЊ.ВЛПМТЧГ§ВЩЙКГЩБОжЎЭтЕФЦфЫћГЩБОЃЌМйЩшУПСОЕЅГЕЕФЪЙгУЪйУќЖМЪЧећФъ.
дЊ.ВЛПМТЧГ§ВЩЙКГЩБОжЎЭтЕФЦфЫћГЩБОЃЌМйЩшУПСОЕЅГЕЕФЪЙгУЪйУќЖМЪЧећФъ.
ЃЈ1ЃЉЗжБ№ЙРМЦ![]() ЁЂ
ЁЂ![]() СНПюГЕаЭЪЙгУЪйУќВЛЕЭгк
СНПюГЕаЭЪЙгУЪйУќВЛЕЭгк![]() ФъЕФИХТЪЃЛ
ФъЕФИХТЪЃЛ
ЃЈ2ЃЉШчЙћФуЪЧ![]() ЙЋЫОЕФИКд№ШЫЃЌвдВЮМгПЦбЇФЃФтВтЪдЕФСНПюГЕаЭИї
ЙЋЫОЕФИКд№ШЫЃЌвдВЮМгПЦбЇФЃФтВтЪдЕФСНПюГЕаЭИї![]() СОЕЅГЕВњЩњРћШѓЕФЦНОљЪ§ЮЊОіВпвРОнЃЌФуЛсбЁдёВЩЙКФФПюГЕаЭЃП
СОЕЅГЕВњЩњРћШѓЕФЦНОљЪ§ЮЊОіВпвРОнЃЌФуЛсбЁдёВЩЙКФФПюГЕаЭЃП
ЁОД№АИЁПЃЈ1ЃЉ0.8ЃЌ0.9ЃЈ2ЃЉгІИУВЩЙК![]() ПюЕЅГЕ
ПюЕЅГЕ
ЁОНтЮіЁПЗжЮіЃК(1)ИљОнЬтжаЫљИјЕФЭМБэЃЌДгжаЕУЕНЪйУќВЛЕЭгкСНФъЕФга80СОЃЌРћгУЙЋЪНЧѓЕУЯргІЕФИХТЪЃЛ
(2)РћгУЙЋЪНЧѓЕУет100СОГЕЕФзмРћШѓЃЌГ§вд100ЮЊЦНОљРћШѓЃЌЭЈЙ§БШНЯДѓаЁЕУЕНЯргІЕФНсТл.
ЯъНтЃКЃЈ1ЃЉвђЮЊ![]() СО
СО![]() ПюГЕаЭжага
ПюГЕаЭжага![]() СОЪЙгУЪйУќВЛЕЭгк
СОЪЙгУЪйУќВЛЕЭгк![]() ФъЃЌ
ФъЃЌ
ЫљвдЙРМЦ![]() ПюГЕаЭЪЙгУЪйУќВЛЕЭгк
ПюГЕаЭЪЙгУЪйУќВЛЕЭгк![]() ФъЕФИХТЪЮЊЃК
ФъЕФИХТЪЮЊЃК![]() ЃЛ
ЃЛ
ЫљвдвђЮЊ![]() СО
СО![]() ПюГЕаЭжага
ПюГЕаЭжага![]() СОЪЙгУЪйУќВЛЕЭгк
СОЪЙгУЪйУќВЛЕЭгк![]() ФъЃЌ
ФъЃЌ
ЙРМЦ![]() ПюГЕаЭЪЙгУЪйУќВЛЕЭгк
ПюГЕаЭЪЙгУЪйУќВЛЕЭгк![]() ФъЕФИХТЪЮЊЃК
ФъЕФИХТЪЮЊЃК![]() .
.
ЃЈ2ЃЉУПЩњВњ![]() СО
СО![]() ПюГЕПЩВњЩњРћШѓЕФЦНОљжЕЮЊЃК
ПюГЕПЩВњЩњРћШѓЕФЦНОљжЕЮЊЃК
![]()
![]()
![]() ЃЈдЊЃЉ.
ЃЈдЊЃЉ.
УПЩњВњ![]() СО
СО![]() ПюГЕПЩВњЩњРћШѓЕФЦНОљжЕЮЊЃК
ПюГЕПЩВњЩњРћШѓЕФЦНОљжЕЮЊЃК
![]()
![]()
![]() ЃЈдЊЃЉ.
ЃЈдЊЃЉ.
Ёп![]() ЃЌЁргІИУВЩЙК
ЃЌЁргІИУВЩЙК![]() ПюЕЅГЕ.
ПюЕЅГЕ.


 ПЊаФПьРжМйЦкзївЕЪюМйзївЕЮїАВГіАцЩчЯЕСаД№АИ
ПЊаФПьРжМйЦкзївЕЪюМйзївЕЮїАВГіАцЩчЯЕСаД№АИ УћЬтбЕСЗЯЕСаД№АИ
УћЬтбЕСЗЯЕСаД№АИ ЦкФЉМЏНсКХЯЕСаД№АИ
ЦкФЉМЏНсКХЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЖрУцЬх![]() жа,
жа, ![]() ЦНУц
ЦНУц![]() ,
,![]() ,ЫФБпаЮ
,ЫФБпаЮ![]() ЪЧБпГЄЮЊ
ЪЧБпГЄЮЊ![]() ЕФСтаЮ.
ЕФСтаЮ.

ЃЈ1ЃЉжЄУї: ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЯпЖЮ![]() ЩЯЪЧЗёДцдкЕу
ЩЯЪЧЗёДцдкЕу![]() ,ЪЙ
,ЪЙ![]() ЦНУц
ЦНУц![]() ,ШєДцдк,Чѓ
,ШєДцдк,Чѓ![]() ЕФжЕЃЛШєВЛДцдк,ЧыЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдк,ЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтДКМОжчвЙЮТВюДѓаЁгыФГжжзгЗЂбПЖрЩйжЎМфЕФЙиЯЕЃЌЯждкДг4дТЗнЕФ30ЬьжаЫцЛњЬєбЁСЫ5ЬьНјаабаОПЃЌЧвЗжБ№МЧТМСЫУПЬьжчвЙЮТВюгыУПЬь100ПХжжзгНўХнКѓЕФЗЂбПЪ§ЃЌЕУЕНШчЯТзЪСЯЃК
ШеЦк | 4дТ1Ше | 4дТ7Ше | 4дТ15Ше | 4дТ21Ше | 4дТ30Ше |
ЮТВюx/Ёц | 10 | 11 | 13 | 12 | 8 |
ЗЂбПЪ§y/ПХ | 23 | 25 | 30 | 26 | 16 |
ЃЈЂёЃЉДгет5ЬьжаШЮбЁ2ЬьЃЌМЧЗЂбПЕФжжзгЪ§ЗжБ№ЮЊmЃЌnЃЌЧѓЪТМўЁАmЃЌnОљВЛаЁгк25ЁБЕФИХТЪЃЎ
ЃЈЂђЃЉДгет5ЬьжаШЮбЁ2ЬьЃЌШєбЁШЁЕФЪЧ4дТ1Шегы4дТ30ШеЕФСНзщЪ§ОнЃЌЧыИљОнет5ЬьжаЕФСэ3ЬьЕФЪ§ОнЃЌЧѓГіyЙигкxЕФЯпадЛиЙщЗНГЬ ![]() =
= ![]() x+
x+ ![]() ЃЎ
ЃЎ
ЃЈВЮПМЙЋЪНЃК ![]() =
=  ЃЌ
ЃЌ ![]() =
= ![]() Љ
Љ ![]()
![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉ= ![]()
ЃЈ1ЃЉСюNЃЈxЃЉ=ЃЈ1+xЃЉ2Љ1+lnЃЈ1+xЃЉЃЌХаЖЯВЂжЄУїNЃЈxЃЉдкЃЈЉ1ЃЌ+ЁоЃЉЩЯЕФЕЅЕїадЃЌВЂЧѓNЃЈ0ЃЉЃЛ
ЃЈ2ЃЉЧѓfЃЈxЃЉдкЖЈвхгђЩЯЕФзюаЁжЕЃЛ
ЃЈ3ЃЉЪЧЗёДцдкЪЕЪ§mЃЌnТњзу0ЁмmЃМnЃЌЪЙЕУfЃЈxЃЉдкЧјМф[mЃЌn]ЩЯЕФжЕгђвВЮЊ[mЃЌn]ЃП ЃЈВЮПМЙЋЪНЃК[lnЃЈ1+xЃЉЁф]= ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() Й§Еу
Й§Еу![]() ЃЌЦфВЮЪ§ЗНГЬЮЊ
ЃЌЦфВЮЪ§ЗНГЬЮЊ ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЌ
ЮЊВЮЪ§ЃЌ ![]() ЃЉЃЌвд
ЃЉЃЌвд![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ ![]() жсЗЧИКАыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсЗЧИКАыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЦеЭЈЗНГЬКЭЧњЯп
ЕФЦеЭЈЗНГЬКЭЧњЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉЧѓвбжЊЧњЯп![]() КЭЧњЯп
КЭЧњЯп![]() НЛгк
НЛгк![]() СНЕуЃЌЧв
СНЕуЃЌЧв![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВCЃК![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃК
ЃК![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШєжБЯп![]() БЛдВCНиЕУЕФЯвГЄЮЊ
БЛдВCНиЕУЕФЯвГЄЮЊ![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЕБt =1ЪБЃЌгЩжБЯп![]() ЩЯЕФЖЏЕуPв§дВCЕФСНЬѕЧаЯпЃЌШєЧаЕуЗжБ№ЮЊAЃЌBЃЌдђжБЯпABЪЧЗёКуЙ§вЛИіЖЈЕуЃПШєДцдкЃЌЧѓГіИУЖЈЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЩЯЕФЖЏЕуPв§дВCЕФСНЬѕЧаЯпЃЌШєЧаЕуЗжБ№ЮЊAЃЌBЃЌдђжБЯпABЪЧЗёКуЙ§вЛИіЖЈЕуЃПШєДцдкЃЌЧѓГіИУЖЈЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФДЙжБЦНЗжЯпЃЌ
ЕФДЙжБЦНЗжЯпЃЌ![]() гы
гы![]() НЛгыЕу
НЛгыЕу![]() ЮЊ
ЮЊ![]() ЩЯвьгк
ЩЯвьгк![]() ЕФШЮвтвЛЕу.
ЕФШЮвтвЛЕу.

![]() Чѓ
Чѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
![]() ХаЖЯ
ХаЖЯ![]() ЕФжЕЪЧЗёЮЊвЛИіГЃЪ§ЃЌВЂЫЕУїРэгЩЃЎ
ЕФжЕЪЧЗёЮЊвЛИіГЃЪ§ЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЧ![]() БэЪОДѓгк
БэЪОДѓгк![]() ЕФећЪ§
ЕФећЪ§![]() ЕФЪЎЮЛЪ§ЃЌР§Шч
ЕФЪЎЮЛЪ§ЃЌР§Шч![]() ЃЌ
ЃЌ![]() .вбжЊ
.вбжЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЖМЪЧДѓгк
ЖМЪЧДѓгк![]() ЕФЛЅВЛЯрЕШЕФећЪ§ЃЌЯжгаШчЯТ
ЕФЛЅВЛЯрЕШЕФећЪ§ЃЌЯжгаШчЯТ![]() ИіУќЬтЃК
ИіУќЬтЃК
ЂйШє![]() ЃЌдђ
ЃЌдђ![]() ЃЛЂк
ЃЛЂк![]() ЃЌ
ЃЌ![]() Чв
Чв![]() ЃЛ
ЃЛ
ЂлШє![]() ЪЧжЪЪ§ЃЌдђ
ЪЧжЪЪ§ЃЌдђ![]() вВЪЧжЪЪ§ЃЛЂмШє
вВЪЧжЪЪ§ЃЛЂмШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ГЩЕШВюЪ§СаЃЌдђ
ГЩЕШВюЪ§СаЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ПЩФмГЩЕШБШЪ§Са.
ПЩФмГЩЕШБШЪ§Са.
ЦфжаЫљгаЕФецУќЬтЮЊЃЈ ЃЉ
A. Ђк B. ЂлЂм C. ЂйЂкЂм D. ЂйЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжДааШчЭМЫљЪОЕФГЬађПђЭМЃЌЪфГіЕФSжЕЮЊЃЈЁЁЁЁЃЉ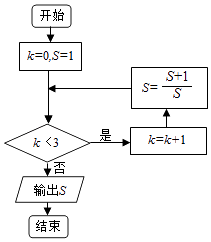
A.2
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com