
【题目】已知一工厂生产了某种产品700件,该工厂需要对这些产品的性能进行检测现决定利用随机数表法从中抽取100件产品进行抽样检测,将700件产品按001,002,…,700进行编号
(1)如果从第8行第4列的数开始向右读,请你依次写出最先检测的3件产品的编号;(下面摘取了随机数表的第7~9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)检测结果分为优等、合格、不合格三个等级,抽取的100件产品的安全性能和环保性能的检测结果如下表(横向和纵向分别表示安全性能和环保性能):
(i)若在该样本中,产品环保性能是优等的概率为34%,求![]() 的值;
的值;
(ii)若![]() ,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率.
,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率.
件数 | 环保性能 | |||
优等 | 合格 | 不合格 | ||
安全性能 | 优等 | 6 | 20 | 5 |
合格 | 10 | 18 | 6 | |
不合格 | m | 4 | n | |
科目:高中数学 来源: 题型:
【题目】某工厂生产的10件产品中,有8件合格品、2件不合格品,合格品与不合格品在外观上没有区别.从这10件产品中任意抽检2件,计算:
(1)抽出的2件产品恰好都是合格品的抽法有多少种?
(2)抽出的2件产品至多有1件不合格品的抽法有多少种?
(3)如果抽检的2件产品都是不合格品,那么这批产品将被退货,求这批产品被退货的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() 满足:
满足:![]() (
(![]() 为常数,且
为常数,且![]() ,
,![]() ).
).
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,若数列
,若数列![]() 为等比数列,求
为等比数列,求![]() 的值;
的值;
(3)在满足条件(2)的情形下,设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若不等式
,若不等式![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由国家公安部提出,国家质量监督检验检疫总局发布的《车辆驾驶人员血液、呼气酒精含量阀值与检验标准(GB/T19522-2010)》于2011年7月1日正式实施.车辆驾驶人员酒饮后或者醉酒后驾车血液中的酒精含量阀值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,且图表示的函数模型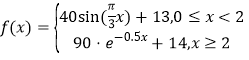 ,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:
,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:![]() ,
,![]() )
)
驾驶行为类型 | 阀值 |
饮酒后驾车 |
|
醉酒后驾车 |
|
车辆驾车人员血液酒精含量阀值
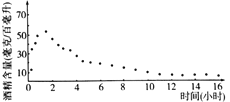
喝1瓶啤酒的情况
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com