
分析 可分别取AB,AC的中点D,E,并连接OD,OE,从而有OD⊥AB,OE⊥AC,而由余弦定理可以得到cos∠BAC=$\frac{1}{4}$.对等式$\overrightarrow{AO}=p\overrightarrow{AB}+q\overrightarrow{AC}$的两边分别乘向量$\overrightarrow{AB},\overrightarrow{AC}$,进行数量积的运算便可得出关于p,q的方程组:$\left\{\begin{array}{l}{2=4p+\frac{3}{2}q}\\{\frac{9}{2}=\frac{3}{2}p+9q}\end{array}\right.$,解方程组便可得出p,q的值.
解答 解:如图,取AB中点D,AC中点E,连接OD,OE,则OD⊥AB,OE⊥AC;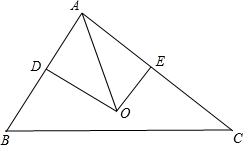
在△ABC中,AB=2,BC=$\sqrt{10}$,AC=3;
∴由余弦定理得,$cos∠BAC=\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}$=$\frac{4+9-10}{12}=\frac{1}{4}$;
由$\overrightarrow{AO}=p\overrightarrow{AB}+q\overrightarrow{AC}$得:$\left\{\begin{array}{l}{\overrightarrow{AO}•\overrightarrow{AB}=p{\overrightarrow{AB}}^{2}+q\overrightarrow{AC}•\overrightarrow{AB}}\\{\overrightarrow{AO}•\overrightarrow{AC}=p\overrightarrow{AB}•\overrightarrow{AC}+q{\overrightarrow{AC}}^{2}}\end{array}\right.$;
$\overrightarrow{AO}•\overrightarrow{AB}=|\overrightarrow{AO}||\overrightarrow{AB}|cos∠BAO$=$|\overrightarrow{AB}||\overrightarrow{AD}|=2×1=2$,$\overrightarrow{AO}•\overrightarrow{AC}=|\overrightarrow{AC}||\overrightarrow{AE}|=3×\frac{3}{2}=\frac{9}{2}$;
∴$\left\{\begin{array}{l}{2=4p+\frac{3}{2}q}\\{\frac{9}{2}=\frac{3}{2}p+9q}\end{array}\right.$;
解得$p=\frac{1}{3},q=\frac{4}{9}$.
点评 考查三角形外心的定义,余弦定理,以及数量积的运算及其计算公式,余弦函数的定义.


科目:高中数学 来源: 题型:选择题
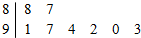 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91.5、5 | B. | 91、5 | C. | 92、5.5 | D. | 92、5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f({\frac{π}{3}})>\sqrt{2}f({\frac{π}{4}})$ | B. | $f({\frac{π}{3}})>2cos1•f(1)$ | C. | $f({\frac{π}{4}})<\sqrt{2}cos1•f(1)$ | D. | $f({\frac{π}{4}})<\frac{{\sqrt{6}}}{2}f({\frac{π}{6}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {2,3} | C. | ∅ | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com