
分析 根据二次函数的性质,先求出函数的单调性,从而分别求出区间是上的最值即可.
解答 解:y=x2+4x-2=(x+2)2-6,
(1)y≥-6,∴y=x2+4x-2,x∈R时的值域是:[-6,+∞);
(2)函数在[-5,-2)递减,在(-2,0]递增,
∴x=-2时,函数值最小,x=-5时,函数值最大,
∴函数的最小值是-6,最大值是3,
∴y=x2+4x-2,x∈[-5,0]的值域是:[-6,3];
(3)函数在[-6,-3]递减,
∴x=-6时,函数值最大,x=-3时,函数值最小,
∴最大值是10,最小值是-5;
∴y=x2+4x-2,x∈[-6,-3]的值域是:[-5,10];
(4)函数在[0,2]递增,
∴x=0时,函数值直最小,x=2时,函数值最大,
∴最大值是10,最小值是-2,
∴y=x2+4x-2,x∈[0,2]的值域是:[-2,10].
点评 本题考查了二次函数的性质,考查函数的单调性、最值问题,是一道基础题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源:2017届安徽淮北十二中高三上月考二数学(文)试卷(解析版) 题型:解答题
已知命题 函数
函数 在区间
在区间 上有1个零点;命题
上有1个零点;命题 函数
函数 与
与 轴交于不同的两点,如果
轴交于不同的两点,如果 是假命题,
是假命题, 是真命题,求
是真命题,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届安徽淮北十二中高三上月考二数学(理)试卷(解析版) 题型:解答题
已知命题 关于
关于 的方程
的方程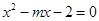 在
在 有解,命题
有解,命题 在
在 单调递增;若
单调递增;若 为真命题,
为真命题, 是真命题,求实数
是真命题,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②全错 | B. | ①对②错 | C. | ①错②对 | D. | ①②全对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$P | B. | $\frac{1}{2}$-P | C. | 1-2P | D. | 1-P |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com