
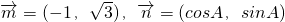 ,且
,且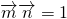
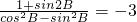 ,求tanB.
,求tanB. (-1,
(-1, ),
), (cosA,sinA),且
(cosA,sinA),且 •
• =1,
=1, sinA-cosA=2(
sinA-cosA=2( sinA-
sinA- cosA)=2sin(A-
cosA)=2sin(A- )=1,
)=1, )=
)= ,
, <A-
<A- <
< ,
, =
= ,
, ;
;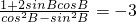 ,且sin2B+cos2B=1,
,且sin2B+cos2B=1, •
• =1,利用平面向量的数量积运算法则列出关系式,关系式左边提取2,利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,求出这个正弦函数的函数值,由A为三角形的内角,求出这个角的范围,利用特殊角的三角函数值即可求出A的度数;
=1,利用平面向量的数量积运算法则列出关系式,关系式左边提取2,利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,求出这个正弦函数的函数值,由A为三角形的内角,求出这个角的范围,利用特殊角的三角函数值即可求出A的度数;

科目:高中数学 来源:2010年高考试题(湖北卷)解析版(理) 题型:选择题
记实数 中的最大数为
中的最大数为 ,最小数为
,最小数为 已知
已知 的三边边长为a,b,c(
的三边边长为a,b,c( ),定义它的倾斜度为
),定义它的倾斜度为

则 是“
是“ 为等边三角”的
为等边三角”的
A.必要而不充分的条件 B.充分而不必要的条件
C.充要条件 D.既不充分也不必要的条件
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| AB |
| AB |
| AC |
| AB |
| CB |
| BC |
| CA |
| A.等腰三角形 |
| B.直角三角开 |
| C.等腰直角三角形 |
| D.既非等腰三角形又非直角三角形 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海外国语大学附中高三(上)第一次周练数学试卷(解析版) 题型:选择题
 ,则△ABC为( )
,则△ABC为( )查看答案和解析>>
科目:高中数学 来源:2005-2006学年湖北省武汉市华中师大一附中高三(上)期中数学试卷(理科)(解析版) 题型:选择题
 ,则△ABC为( )
,则△ABC为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com