
【题目】中国共产党第十九次全国代表大会于2017年10月18日至10月24日在北京召开,会议提出“决胜全面建成小康社会”.某市积极响应开展“脱贫攻坚”,为2020年“全面建成小康社会”贡献力量.为了解该市农村“脱贫攻坚”情况,从某县调查得到农村居民2013年至2017年家庭人均纯收入![]() (单位:百元)的数据如表:
(单位:百元)的数据如表:
年 份 | 2013 | 2014 | 2015 | 2016 | 2017 |
年人均纯收入 | 47 | 55 | 61 | 65 | 72 |
注:小康的标准是农村居民家庭年人均纯收入达到8000元.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,预测2020年该县农村居民家庭年人均纯收入指标能否达到“全面建成小康社会”的标准?
附:回归直线![]() 斜率和截距的最小二乘估计公式分别为:
斜率和截距的最小二乘估计公式分别为:
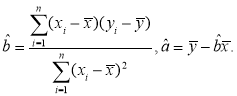
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
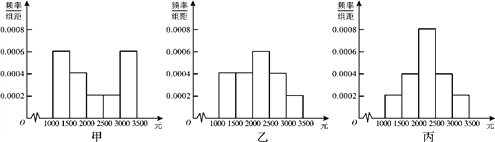
【题目】为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1、s2、s3,则它们的大小关系为__________.(用“>”连接)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年冬,北京雾霾天数明显减少,据环保局统计三个月的空气质量,达到优良的天数超过70天.重度污染的天数仅有4天.主要原因是政府对治理雾霾采取了有效措施,如①减少机动车尾气排放;②实施了煤改电或煤改气工程;③关停了大量的排污企业;④部分企业季节性的停产.为了解农村地区实施煤改气工程后天然气使用情况,从某乡镇随机抽取100户,进行均用气量调查,得到的用气量数据(单位:千立方米)均在区间![]() 围内,将数据按区间列表如下:
围内,将数据按区间列表如下:
分组 | 频数 | 频率 |
| 14 | 0.14 |
|
|
|
| 55 | 0.55 |
| 4 | 0.04 |
| 2 | 0.02 |
合计 | 100 | 1 |
(1)求表中![]() ,
,![]() 的值;
的值;
(2)若同组中的每个数据用该组区间中点值代替,估计该乡每户月平均用气量;
(3)从用量高于3千立方米的用户中任选2户,进行燃气使用的满意度调查,求这2户用气量处于不同区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数).
为常数).
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)是否存在正实数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,若存在,求出实数
,若存在,求出实数![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(Ⅲ)当![]() 时,
时, ![]() ,对
,对![]() 恒成立,求整数
恒成立,求整数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的![]() ,纵坐标不变,再向右平移
,纵坐标不变,再向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )
A. 函数![]() 的一条对称轴是
的一条对称轴是![]()
B. 函数![]() 的一个对称中心是
的一个对称中心是![]()
C. 函数![]() 的一条对称轴是
的一条对称轴是![]()
D. 函数![]() 的一个对称中心是
的一个对称中心是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学名著《算学启蒙》中有关于“松竹并生”的问题:松长四尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图,是源于其思想的一个程序框图.若输入的![]() 分别为8、2,则输出的
分别为8、2,则输出的![]() ( )
( )
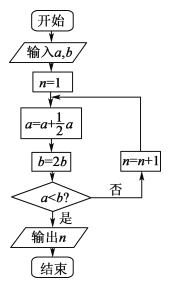
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】了应对新疆暴力恐怖活动,重庆市警方从武警训练基地挑选反恐警察,从体能、射击、反应三项指标进行检测,如果这三项中至少有两项通过即可入选.假定某基地有4名武警战士(分别记为![]() )拟参加挑选,且每人能通过体能、射击、爆破的概率分别为
)拟参加挑选,且每人能通过体能、射击、爆破的概率分别为![]() .这三项测试能否通过相互之间没有影响.
.这三项测试能否通过相互之间没有影响.
(1)求![]() 能够入选的概率;
能够入选的概率;
(2)规定:按入选人数得训练经费,每入选1人,则相应的训练基地得到5000元的训练经费,求该基地得到训练经费的分布列与数学期望(期望精确到个位).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com