
【题目】已知抛物线的方程为y2=4x,直线L过定点P(﹣2,1),斜率为k.当k为何值时直线与抛物线:
(1)只有一个公共点;
(2)有两个公共点;
(3)没有公共点.
【答案】
(1)解:由题意可设直线方程为:y=k(x+2)+1,
代入抛物线方程整理可得k2x2+(4k2+2k﹣4)x+4k2+4k+1=0(*)
直线与抛物线只有一个公共点等价于(*)只有一个根
①k=0时,y=1符合题意;
②k≠0时,△=(4k2+2k﹣4)2﹣4k2(4k2+4k+1)=0,整理,得2k2+k﹣1=0,
解得k= ![]() 或k=﹣1.
或k=﹣1.
综上可得,k= ![]() 或k=﹣1或k=0
或k=﹣1或k=0
(2)解:由(1)得2k2+k﹣1<0且k≠0,∴﹣1<k< ![]() 且k≠0
且k≠0
(3)解:由(1)得2k2+k﹣1>0,∴k> ![]() 或k<﹣1
或k<﹣1
【解析】设出直线方程代入抛物线方程整理可得k2x2+(4k2+2k﹣4)x+4k2+4k+1=0(*)(1)直线与抛物线只有一个公共点(*)只有一个根(2)直线与抛物线有2个公共点(*)有两个根(3)直线与抛物线没有一个公共点(*)没有根


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知随机变量X服从正态分布N(μ,σ2),且P(μ﹣2σ<X≤μ+2σ)=0.9544,P(μ﹣σ<X≤μ+σ)=0.6826,若μ=4,σ=1,则P(5<X<6)=( )
A.0.1358
B.0.1359
C.0.2716
D.0.2718
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一元二次不等式f(x)<0的解集为{x|x<﹣1或x> ![]() },则f(10x)>0的解集为( )
},则f(10x)>0的解集为( )
A.{x|x<﹣1或x>﹣lg2}
B.{x|﹣1<x<﹣lg2}
C.{x|x>﹣lg2}
D.{x|x<﹣lg2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(x+1)+a(x2﹣x),a≥0.
(1)当a=1时,求函数f(x)的极值;
(2)若x>0,f(x)≥0成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a2x﹣2﹣x定义域为R的奇函数.
(1)求实数a的值;
(2)判断函数f(x)在R上的单调性,并利用函数单调性的定义证明;
(3)若不等式f(9x+1)+f(t﹣23x+5)>0在在R上恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=sin (2x+ ![]() )的图象可由函数y=cosx的图象( )
)的图象可由函数y=cosx的图象( )
A.先把各点的横坐标缩短到原来的 ![]() 倍,再向左平移
倍,再向左平移 ![]() 个单位
个单位
B.先把各点的横坐标缩短到原来的 ![]() 倍,再向右平移
倍,再向右平移 ![]() 个单位
个单位
C.先把各点的横坐标伸长到原来的2倍,再向左平移 ![]() 个单位
个单位
D.先把各点的横坐标伸长到原来的2倍,再向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,AD⊥AF,AE=AD=2. 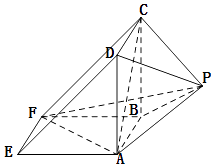
(Ⅰ)证明:平面PAD⊥平面ABFE;
(Ⅱ)求正四棱锥P﹣ABCD的高h,使得二面角C﹣AF﹣P的余弦值是 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 是定义域在R上的奇函数,且f(2)=
是定义域在R上的奇函数,且f(2)= ![]() .
.
(1)求实数a、b的值;
(2)判断函数f(x)的单调性,并用定义证明;
(3)解不等式:f(log ![]() (2x﹣2)]+f[log2(1﹣
(2x﹣2)]+f[log2(1﹣ ![]() x)]≥0.
x)]≥0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com