
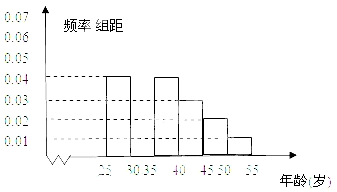
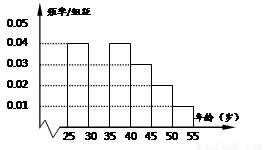
 某班同学在“十八大”期间进行社会实践活动,对[25,55]岁的人群随机抽取n人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
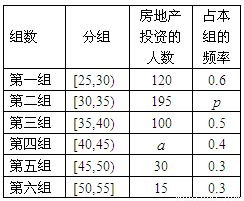
某班同学在“十八大”期间进行社会实践活动,对[25,55]岁的人群随机抽取n人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:| 组数 | 分组 | 房地产投资的人数 | 占本组的频率 |
| 第一组] | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
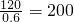 ,由频率分布直方图可得其频率为0.04×5=0.2,因此共抽取的人数n=
,由频率分布直方图可得其频率为0.04×5=0.2,因此共抽取的人数n=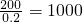 ,
,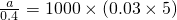 ,解得a=60.
,解得a=60.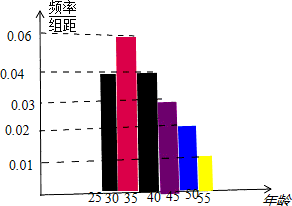
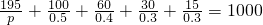 ,得到p=0.65.故第二组的频率为
,得到p=0.65.故第二组的频率为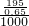 =0.3,其
=0.3,其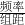 =
=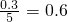 .
.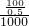 =0.2,其
=0.2,其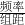 =
=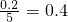 .
.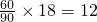 ,
,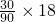 =6.
=6.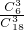 =
= ,P(X=1)=
,P(X=1)= =
= ,P(X=2)=
,P(X=2)= =
= ,P(X=3)=
,P(X=3)= =
= .
.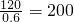 ,及由频率分布直方图可得其频率为0.04×5=0.2,因此共抽取的人数n=
,及由频率分布直方图可得其频率为0.04×5=0.2,因此共抽取的人数n=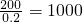 .由频率分布直方图可得第四组的频率,进而得到总人数,即可得到a.再由等式200+
.由频率分布直方图可得第四组的频率,进而得到总人数,即可得到a.再由等式200+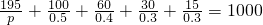 ,可得到得到p.即可得到频率和
,可得到得到p.即可得到频率和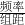 .第三组如此.
.第三组如此. (k=0,1,2,3)即可得到分布列和EX.
(k=0,1,2,3)即可得到分布列和EX.

科目:高中数学 来源: 题型:
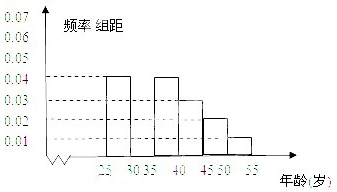 某班同学在“十八大”期间进行社会实践活动,对[25,55]岁的人群随机抽取n人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
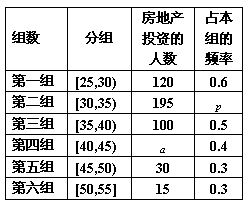
某班同学在“十八大”期间进行社会实践活动,对[25,55]岁的人群随机抽取n人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:| 组数 | 分组 | 房地产投资的人数 | 占本组的频率 |
| 第一组] | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省吉林市高三三模(期末)理科数学试卷(解析版) 题型:解答题
某班同学在“十八大”期间进行社会实践活动,对[25,55]岁的人群随机抽取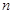 人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
(Ⅰ)求n,a,p的值;
(Ⅱ)从年龄在[40,50)岁的“房地产投资”人群中采取分层抽样法抽取9人参加投资管理学习活动,其中选取3人作为代表发言,记选取的3名代表中年龄在[40,45)岁的人数为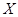 ,求
,求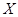 的分布列和期望
的分布列和期望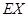 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
某班同学在“十八大”期间进行社会实践活动,对[25,55]岁的人群随机抽取![]() 人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
(Ⅰ)求n,a,p的值;
(Ⅱ)从年龄在[40,50)岁的“房地产投资”人群中采取分层抽样法抽取9人参加投资管理学习活动,其中选取3人作为代表发言,记选取的3名代表中年龄在[40,45)岁的人数为![]() ,求
,求![]() 的分布列和期望
的分布列和期望![]() .
.
 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com