
【题目】某企业生产了一种新产品,在推广期邀请了100位客户试用该产品,每人一台.试用一个月之后进行回访,由客户先对产品性能作出“满意”或“不满意”的评价,再让客户决定是否购买该试用产品(不购买则可以免费退货,购买则仅需付成本价).经统计,决定退货的客户人数是总人数的一半,“对性能满意”的客户比“对性能不满意”的客户多10人,“对性能不满意”的客户中恰有![]() 选择了退货.
选择了退货.
(1)请完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“客户购买产品与对产品性能满意之间有关”.
的把握认为“客户购买产品与对产品性能满意之间有关”.
对性能满意 | 对性能不满意 | 合计 | |
购买产品 | |||
不购买产品 | |||
合计 |
(2)企业为了改进产品性能,现从“对性能不满意”的客户中按是否购买产品进行分层抽样,随机抽取6位客户进行座谈.座谈后安排了抽奖环节,共有4张奖券,奖券上分别印有200元、400元、600元和800元字样,抽到奖券可获得相应奖金.6位客户有放回的进行抽取,每人随机抽取一张奖券,求6位客户中购买产品的客户人均所得奖金不少于500元的概率.
附:![]() ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)详见解析(2)详见解析
【解析】
(1) 根据题意填写列联表,由表中数据计算观测值,对照临界值得出结论;
(2)利用古典概型概率公式即可得到结果.
(1)设“对性能不满意”的客户中购买产品的人数为![]() ,则退货的人数为
,则退货的人数为![]() ,由此可列出下表
,由此可列出下表
对性能满意 | 对性能不满意 | 合计 | |
购买产品 |
| 50 | |
不购买产品 |
| 50 | |
合计 |
|
| 100 |
因为![]() ,所以
,所以![]() ;
;
填写![]() 列联表如下:
列联表如下:
对性能满意 | 对性能不满意 | 合计 | |
购买产品 | 35 | 15 | 50 |
不购买产品 | 20 | 30 | 50 |
合计 | 55 | 45 | 100 |
所以![]()
![]() .
.
所以,有![]() 的把握认为“客户购买产品与对产品性能满意之间有关”.
的把握认为“客户购买产品与对产品性能满意之间有关”.
(2)由题意知:参加座谈的购买产品的人数为2,退货的人数为4.
“购买产品的客户抽取奖券”的基本事件有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共有16个基本事件:
,共有16个基本事件:
设事件![]() “购买产品的客户人均所得奖金不少于500元”,
“购买产品的客户人均所得奖金不少于500元”,
则事件![]() 包含的基本事件有:
包含的基本事件有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共有10个基本事件:
,共有10个基本事件:
则![]() .
.
所以,购买产品的客户人均所得奖金不少于500元的概率是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的最小值
的最小值![]() ;
;
(2)是否存在实数![]() ,
,![]() 同时满足下列条件:①
同时满足下列条件:①![]() ;②当
;②当![]() 的定义域为
的定义域为![]() 时,其值域为
时,其值域为![]() .若存在,求出
.若存在,求出![]() ,
,![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把![]() ,
,![]() ,
,![]() ,
,![]() 四本不同的书分给三位同学,每人至少分到一本,每本书都必须有人分到,
四本不同的书分给三位同学,每人至少分到一本,每本书都必须有人分到,![]() ,
,![]() 不能同时分给同一个人,则不同的分配方式共有__________种(用数字作答).
不能同时分给同一个人,则不同的分配方式共有__________种(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义域为
定义域为![]() ,设
,设![]() .
.
(1)试确定![]() 的取值范围,使得函数
的取值范围,使得函数![]() 在
在![]() 上为单调函数;
上为单调函数;
(2)求证:![]() ;
;
(3)求证:对于任意的![]() ,总存在
,总存在![]() ,满足
,满足![]() ,并确定这样的
,并确定这样的![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() -x2+ef′(
-x2+ef′(![]() )x.
)x.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若存在x1,x2(x1<x2),使得f(x1)+f(x2)=1,求证:x1+x2<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 的导函数
的导函数![]() 的图象如图所示,则以下关于函数
的图象如图所示,则以下关于函数![]() 的判断:
的判断:
①在区间![]() 内单调递增;
内单调递增;
②在区间![]() 内单调递减;
内单调递减;
③在区间![]() 内单调递增;
内单调递增;
④![]() 是极小值点;
是极小值点;
⑤![]() 是极大值点.
是极大值点.
其中正确的是( )
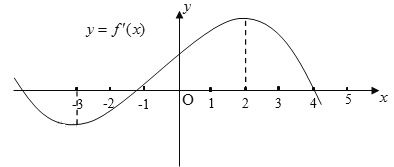
A. ③⑤B. ②③C. ①④⑤D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com