
| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
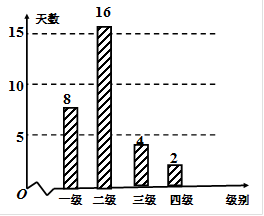
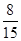 ;
;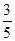 .
.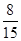 ;
;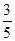 .
.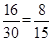 ;
;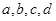 ;样本中空气质量级别为四级的有2天,设其编号为
;样本中空气质量级别为四级的有2天,设其编号为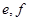 ,则基本事件有:
,则基本事件有: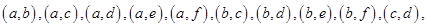
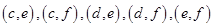 共15个,其中至少有一天空气质量类别为中度污染的情况有:
共15个,其中至少有一天空气质量类别为中度污染的情况有: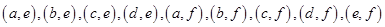 共9个,所以至少有一天空气质量类别为中度污染的概率为
共9个,所以至少有一天空气质量类别为中度污染的概率为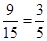 .
.

科目:高中数学 来源:不详 题型:解答题

 天,晴
天,晴 天,雨
天,雨 天,雪
天,雪 天,阴
天,阴 天,其它2天,合计天数为:
天,其它2天,合计天数为: 天.
天. 的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为
的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为 元或
元或 元;在非雨雪天的情况下,他以
元;在非雨雪天的情况下,他以 的概率骑自行车上班,每天交通费用
的概率骑自行车上班,每天交通费用 元;另外以
元;另外以 的概率打出租上班,每天交通费用
的概率打出租上班,每天交通费用 元.(以频率代替概率,保留两位小数. 参考数据:
元.(以频率代替概率,保留两位小数. 参考数据: )
) (单位:元),求
(单位:元),求 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
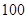 名高一新生分成水平相同的甲、乙两个“平行班”,每班
名高一新生分成水平相同的甲、乙两个“平行班”,每班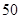 人,吴老师采用
人,吴老师采用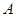 、
、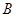 两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取
两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取 名学生的成绩进行统计,作出的茎叶图如下:
名学生的成绩进行统计,作出的茎叶图如下: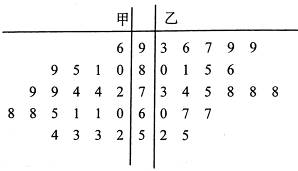
 分者为“成绩优秀”.
分者为“成绩优秀”. 个个体中,从不低于
个个体中,从不低于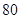 分的成绩中随机抽取
分的成绩中随机抽取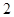 个,记随机变量
个,记随机变量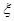 为抽到“成绩优秀”的个数,求
为抽到“成绩优秀”的个数,求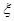 的分布列及数学期望
的分布列及数学期望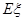 ;
;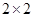 列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?| | 甲班(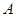 方式) 方式) | 乙班(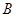 方式) 方式) | 总计 |
| 成绩优秀 | | | |
| 成绩不优秀 | | | |
| 总计 | | | |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
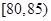 ,
,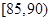 ,
, ,
,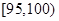 ,
,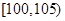 ,
,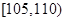 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.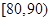 的车辆中任抽取3辆,求抽出的3辆车中车速在
的车辆中任抽取3辆,求抽出的3辆车中车速在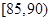 的车辆数
的车辆数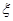 的分布列及数学期望.
的分布列及数学期望.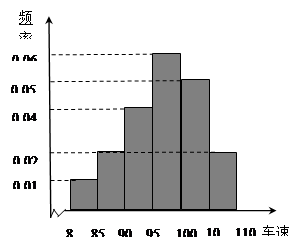
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
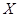 与
与 是否有关系时,通过查阅下表来确定“
是否有关系时,通过查阅下表来确定“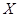 和
和 有关系”的可信度。如果
有关系”的可信度。如果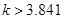 ,那么就有把握认为“
,那么就有把握认为“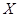 和
和 有关系”的百分比为( )
有关系”的百分比为( ) |  |  |  |  |  |  |  |  |  |  |
 |  |  | 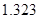 |  |  |  |  |  |  |  |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
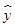 =
=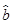 x+
x+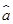 中的
中的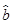 =2,则预测当气温为25 ℃时,冰糕销量为________箱.
=2,则预测当气温为25 ℃时,冰糕销量为________箱.| 气温/℃ | 18 | 13 | 10 | -1 |
| 冰糕/箱 | 64 | 38 | 34 | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com