
【题目】如图,棱形![]() 与正三角形
与正三角形![]() 的边长均为2,它们所在平面互相垂直,
的边长均为2,它们所在平面互相垂直, ![]() ,且
,且![]() .
.
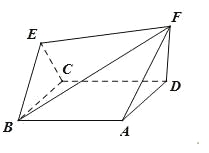
(1)求证: ![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[-1,1]上的奇函数,当x∈[-1,0]时,函数的解析式为f(x)=![]() (a∈R).
(a∈R).
(1)试求a的值;
(2)写出f(x)在[0,1]上的解析式;
(3)求f(x)在[0,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,嵩山上原有一条笔直的山路BC,现在又新架设了一条索道AC,小李在山脚B处看索道AC,发现张角∠ABC=120°;从B处攀登400米到达D处,回头看索道AC,发现张角∠ADC=150°;从D处再攀登800米方到达C处,则索道AC的长为________米.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】5名男生4名女生站成一排,求满足下列条件的排法:
(1)女生都不相邻有多少种排法?
(2)男生甲、乙、丙排序一定(只考虑位置的前后顺序),有多少种排法?
(3)男甲不在首位,男乙不在末位,有多少种排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为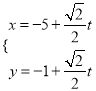 (其中
(其中![]() 为参数),现以坐标原点为极点,
为参数),现以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三点A(-1,1,2),B(1,2,-1),C(a,0,3),是否存在实数a,使A、B、C共线?若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是函数
是函数![]() 的极值点,求函数
的极值点,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(3)在(2)的条件下,是否存在实数![]() ,使得函数
,使得函数![]() 的图象与函数
的图象与函数![]() 的图象恰有
的图象恰有![]() 个交点?若存在,请求出
个交点?若存在,请求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:
摄氏温度/ | -5 | 0 | 4 | 7 | 12 | 15 | 19 | 23 | 27 | 31 | 36 |
热饮杯数 | 156 | 150 | 132 | 128 | 130 | 116 | 104 | 89 | 93 | 76 | 54 |
(1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一般规律;
(3)求回归方程;
(4)如果某天的气温是![]() ,预测这天卖出的热饮杯数.
,预测这天卖出的热饮杯数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com