
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为2的菱形且
是边长为2的菱形且![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)连结![]() ,交
,交![]() 于点
于点![]() ,设
,设![]() 中点为
中点为![]() ,连结
,连结![]() ,
,![]() ,推导出
,推导出![]() ,
,![]() ,且
,且![]() ,从而四边形
,从而四边形![]() 是菱形,进而
是菱形,进而![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() ;(2)推导出
;(2)推导出![]() 是边长为2的等边三角形,设
是边长为2的等边三角形,设![]() 的中点为
的中点为![]() ,连结
,连结![]() ,则
,则![]() ,以
,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,利用向量法能求出二面角
轴,建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
(1)证明:连结![]() ,交
,交![]() 于点
于点![]() ,设
,设![]() 中点为
中点为![]() ,连结
,连结![]() ,
,![]() .
.
∵![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,∴
的中点,∴![]() ,且
,且![]() ,
,
∵![]() ,且
,且![]() ,∴
,∴![]() ,且
,且![]() .
.
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,即
,即![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
∵![]() 是菱形,所以
是菱形,所以![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]()
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)∵![]() ,四边形
,四边形![]() 为菱形.故
为菱形.故![]() 为2的等边三角形.
为2的等边三角形.
设![]() 的中点为
的中点为![]() ,连结
,连结![]() ,则
,则![]() .以
.以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() (如图).
(如图).
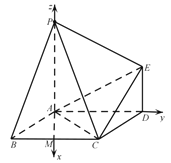
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .设平面
.设平面![]() 的法向量为
的法向量为![]() ,则
,则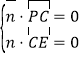 即
即
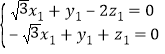 令
令![]() ,则
,则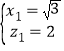 ,所以
,所以![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则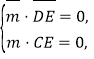 即
即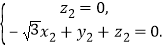
令![]() ,则
,则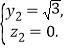 所以
所以![]() .
.
设二面角![]() 的大小为
的大小为![]() ,由于
,由于![]() 为钝角,
为钝角,
所以![]()
![]()


科目:高中数学 来源: 题型:
【题目】已知![]() 三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
(Ⅰ)试估计![]() 班学生人数;
班学生人数;
(Ⅱ)从![]() 班和
班和![]() 班抽出来的学生中各选一名,记
班抽出来的学生中各选一名,记![]() 班选出的学生为甲,
班选出的学生为甲,![]() 班选出的学生为乙,若学生锻炼相互独立,求甲的锻炼时间大于乙的锻炼时间的概率.
班选出的学生为乙,若学生锻炼相互独立,求甲的锻炼时间大于乙的锻炼时间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明![]() 在
在![]() 上是减函数;
上是减函数;
(3)函数![]() 在
在![]() 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O。D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形。沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥。当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义满足不等式|x![]() A|<B(A∈R,B>0)的实数x的集合叫做A的B邻域.若a+b
A|<B(A∈R,B>0)的实数x的集合叫做A的B邻域.若a+b![]() t(t为正常数)的a+b邻域是一个关于原点对称的区间,则a2+b2的最小值为______.
t(t为正常数)的a+b邻域是一个关于原点对称的区间,则a2+b2的最小值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A. ![]() 是向量
是向量![]() ,
,![]() 不共线的充要条件
不共线的充要条件
B. 在空间四边形![]() 中,
中,![]()
C. 在棱长为1的正四面体![]() 中,
中,![]()
D. 设![]() ,
,![]() ,
,![]() 三点不共线,
三点不共线,![]() 为平面
为平面![]() 外一点,若
外一点,若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 四点共面
四点共面
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com