
【题目】已知三点O(0,0),A(﹣2,1),B(2,1),曲线C上任意一点M(x,y)满足| ![]() +
+ ![]() |=
|= ![]() (
( ![]() +
+ ![]() )+2.
)+2.
(1)求曲线C的方程;
(2)动点Q(x0 , y0)(﹣2<x0<2)在曲线C上,曲线C在点Q处的切线为直线l:是否存在定点P(0,t)(t<0),使得l与PA,PB都相交,交点分别为D,E,且△QAB与△PDE的面积之比是常数?若存在,求t的值.若不存在,说明理由.
【答案】
(1)解:由 ![]() =(﹣2﹣x,1﹣y),
=(﹣2﹣x,1﹣y), ![]() =(2﹣x,1﹣y)可得
=(2﹣x,1﹣y)可得 ![]() +
+ ![]() =(﹣2x,2﹣2y),
=(﹣2x,2﹣2y),
∴| ![]() +
+ ![]() |=
|= ![]() ,
, ![]() (
( ![]() +
+ ![]() )+2=(x,y)(0,2)+2=2y+2.
)+2=(x,y)(0,2)+2=2y+2.
由题意可得 ![]() =2y+2,化简可得 x2=4y.
=2y+2,化简可得 x2=4y.
(2)解:假设存在点P(0,t)(t<0),满足条件,则直线PA的方程是y= ![]() ,直线PB的方程是y=
,直线PB的方程是y= ![]()
∵﹣2<x0<2,∴ ![]()
①当﹣1<t<0时, ![]() ,存在x0∈(﹣2,2),使得
,存在x0∈(﹣2,2),使得 ![]()
∴l∥PA,∴当﹣1<t<0时,不符合题意;
②当t≤﹣1时, ![]() ,
, ![]() ,
,
∴l与直线PA,PB一定相交,分别联立方程组
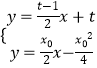 ,
, 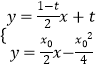 ,解得D,E的横坐标分别是
,解得D,E的横坐标分别是 ![]() ,
, ![]()
∴ ![]()
∵|FP|=﹣ ![]()
∴ ![]() =
= ![]()
∵ ![]()
∴ ![]() =
= ![]() ×
× ![]()
∵x0∈(﹣2,2),△QAB与△PDE的面积之比是常数
∴ ![]() ,解得t=﹣1,
,解得t=﹣1,
∴△QAB与△PDE的面积之比是2.
【解析】(1)用坐标表示 ![]() ,
, ![]() ,从而可得
,从而可得 ![]() +
+ ![]() ,可求|
,可求| ![]() +
+ ![]() |,利用向量的数量积,结合M(x,y)满足|
|,利用向量的数量积,结合M(x,y)满足| ![]() +
+ ![]() |=
|= ![]() (
( ![]() +
+ ![]() )+2,可得曲线C的方程;(2)假设存在点P(0,t)(t<0),满足条件,则直线PA的方程是y=
)+2,可得曲线C的方程;(2)假设存在点P(0,t)(t<0),满足条件,则直线PA的方程是y= ![]() ,直线PB的方程是y=
,直线PB的方程是y= ![]() 分类讨论:①当﹣1<t<0时,l∥PA,不符合题意;②当t≤﹣1时,
分类讨论:①当﹣1<t<0时,l∥PA,不符合题意;②当t≤﹣1时, ![]() ,
, ![]() ,分别联立方程组,解得D,E的横坐标,进而可得△QAB与△PDE的面积之比,利用其为常数,即可求得结论.
,分别联立方程组,解得D,E的横坐标,进而可得△QAB与△PDE的面积之比,利用其为常数,即可求得结论.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】某校高三年级举行了一次全年级的大型考试,在数学成绩优秀和非优秀的学生中,物理、化学、总分成绩也为优秀的人数如下表所示,则我们能以99%的把握认为数学成绩优秀与物理、化学、总分成绩优秀有关系吗?
物理优秀 | 化学优秀 | 总分优秀 | |
数学优秀 | 228 | 225 | 267 |
数学非优秀 | 143 | 156 | 99 |
注:该年级此次考试中数学成绩优秀的有360人,非优秀的有880人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() +bx+c,
+bx+c,
(1)若f(x)在(-∞,+∞)上是增函数,求b的取值范围;
(2)若f(x)在x=1处取得极值,且x∈[-1,2]时,f(x)<c2恒成立,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从A1(1,0,0),A2(2,0,0),B1(0,1,0),B2(0,2,0),C1(0,0,1),C2(0,0,2)这6个点中随机选取3个点,将这3个点及原点O两两相连构成一个“立体”,记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内,此时“立体”的体积V=0). 
(1)求V=0的概率;
(2)求V的分布列及数学期望EV.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2010年至2016年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
年 份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的回归直线方程;
(2)利用(1)中的回归方程,分析2010年至2016年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2018年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个商场经销某种商品,根据以往资料统计,每位顾客采用的分期付款次数![]() 的分布列为:
的分布列为:
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;采用2期或3期付款,其利润为250元;采用4期或5期付款,其利润为300元.![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求购买该商品的3位顾客中,恰有2位采用1期付款的概率;
(2)求![]() 的分布列及期望
的分布列及期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosωx﹣sinωx,sinωx),
=(cosωx﹣sinωx,sinωx), ![]() =(﹣cosωx﹣sinωx,2
=(﹣cosωx﹣sinωx,2 ![]() cosωx),设函数f(x)=
cosωx),设函数f(x)= ![]()
![]() +λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ![]() ,1)
,1)
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点( ![]() ,0)求函数f(x)在区间[0,
,0)求函数f(x)在区间[0, ![]() ]上的取值范围.
]上的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com