
【题目】已知直线过定点P(2,1).
(1)求经过点P且在两坐标轴上的截距相等的直线方程;
(2)若过点P的直线l与x轴和y轴的正半轴分别交于A,B两点,求△AOB面积的最小值及此时直线l的方程.
【答案】
(1)解:∵直线过定点P(2,1)且在两坐标轴上的截距相等,
设直线方程为:x+y=a,将P(2,1)代入得:a=3,
故直线方程是:x+y﹣3=0
(2)解:由题意设直线的截距式方程为 ![]() =1(a,b>0),
=1(a,b>0),
∵直线过P(2,1),∴ ![]() +
+ ![]() =1,
=1,
∴1= ![]() +
+ ![]() ≥2
≥2 ![]() ,∴ab≥8,
,∴ab≥8,
当且仅当 ![]() =
= ![]() 即a=4且b=2时取等号,
即a=4且b=2时取等号,
∴△AOB的面积S= ![]() ab≥4,
ab≥4,
∴△AOB面积的最小值为4,此时直线l的方程为 ![]() =1,
=1,
化为一般式方程可得x+2y﹣4=0
【解析】(1)设出直线的方程,代入P点,求出即可;(2)由题意设直线的截距式方程为 ![]() =1(a,b>0),可得
=1(a,b>0),可得 ![]() +
+ ![]() =1,由基本不等式可得ab≥8,可得△AOB的面积S≥4,可得此时直线的方程.
=1,由基本不等式可得ab≥8,可得△AOB的面积S≥4,可得此时直线的方程.
【考点精析】解答此题的关键在于理解截距式方程的相关知识,掌握直线的截距式方程:已知直线![]() 与
与![]() 轴的交点为A
轴的交点为A![]() ,与
,与![]() 轴的交点为B
轴的交点为B![]() ,其中
,其中![]() .
.


科目:高中数学 来源: 题型:
【题目】对二次函数f(x)=ax2+bx+c(a为非零整数),四位同学分别给出下列结论,其中有且只有一个结论是错误的,则错误的结论是( )
A.﹣1是f(x)的零点
B.1是f(x)的极值点
C.3是f(x)的极值
D.点(2,8)在曲线y=f(x)上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{bn}满足bn=3bn﹣1+2(n≥2),b1=1.数列{an}的前n项和为Sn , 满足Sn=4an+2
(1)求证:{bn+1}是等比数列并求出数列{bn}的通项公式;
(2)求数列{an}的通项公式和前n项和公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=r2(r>0),点P为圆O上任意一点(不在坐标轴上),过点P作倾斜角互补的两条直线分别交圆O于另一点A,B.
(1)当直线PA的斜率为2时,
①若点A的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ),求点P的坐标;
),求点P的坐标;
②若点P的横坐标为2,且PA=2PB,求r的值;
(2)当点P在圆O上移动时,求证:直线OP与AB的斜率之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 是
是![]() 的中点,底面
的中点,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() ,
, ![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 与棱
与棱![]() 交于点
交于点![]() ,平面
,平面![]() 与平面
与平面![]() 交于直线
交于直线![]() .
.
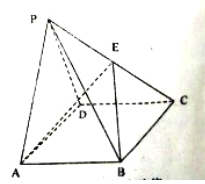
(1)求证: ![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义平面向量之间的一种运算“⊙”如下:对任意的 ![]() ,令
,令 ![]() ,下面说法错误的是( )
,下面说法错误的是( )
A.若 ![]() 与
与 ![]() 共线,则
共线,则 ![]() ⊙
⊙ ![]() =0
=0
B.![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]()
C.对任意的λ∈R,有 ![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]() )
)
D.( ![]() ⊙
⊙ ![]() )2+(
)2+( ![]() )2=|
)2=| ![]() |2|
|2| ![]() |2
|2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,BC边上的高所在的直线方程为x﹣2y+1=0,∠A的角平分线所在的直线方程为y=0,点C的坐标为(1,2).
(1)求点A和点B的坐标;
(2)又过点C作直线l与x轴、y轴的正半轴分别交于点M,N,求△MON的面积最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂随机抽取部分工人调查其上班路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),若上班路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]. 
(1)求直方图中a的值;
(2)如果上班路上所需时间不少于1小时的工人可申请在工厂住宿,若招工2400人,请估计所招工人中有多少名工人可以申请住宿;
(3)该工厂工人上班路上所需的平均时间大约是多少分钟.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com