
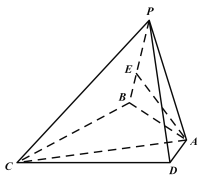
【题目】如图,在四棱锥![]() 中,
中,![]() 是等边三角形,
是等边三角形,![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(2)若![]() ,则在线段
,则在线段![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 平面
平面![]() .若存在,求线段
.若存在,求线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() ,已知曲线
,已知曲线 (
(![]() 为参数),在以
为参数),在以![]() 原点为极点,
原点为极点, ![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,求点
两点,求点![]() 到
到![]() ,
, ![]() 的距离之积。
的距离之积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】跨年迎新联欢晚会简称跨年晚会,是指每年阳历年末12月31日晚上各电视台和政府为喜迎新而精心策划的演唱会活动,跨年晚会首次出现在港台地区,跨年晚会因形式和举办地不同因而名称也不同,如央视启航2020跨年盛典,湖南卫视跨年演唱会,东方卫视迎新晚会等.某电视台为了了解2020年举办的跨年迎新晚会观众的满意度,现分别随机选出![]() 名观众对迎新晚会的质量评估评分,最高分为
名观众对迎新晚会的质量评估评分,最高分为![]() 分,综合得分情况如下表所示:
分,综合得分情况如下表所示:
综合得分 |
|
|
|
|
|
|
|
观众人数 | 5 | 10 | 25 | 30 | 15 | 10 | 5 |
根据表中的数据,回答下列问题:
(1)根据表中的数据,绘制这![]() 位观众打分的频率分布直方图;
位观众打分的频率分布直方图;
(2)已知观众的评分![]() 近似服从
近似服从![]() ,其中
,其中![]() 是反应随机变量
是反应随机变量![]() 取值的平均水平的特征数,工作人员在分析数据时发现,可用
取值的平均水平的特征数,工作人员在分析数据时发现,可用![]() 位观众评分的平均数估计
位观众评分的平均数估计![]() ,但由于评分观众人数较少,误差较大,所以不能直接用
,但由于评分观众人数较少,误差较大,所以不能直接用![]() 位观众评分的标准差的值估计
位观众评分的标准差的值估计![]() ,而在这
,而在这![]() 位观众打分的频率分布直方图的基础上依据
位观众打分的频率分布直方图的基础上依据![]() 来估计
来估计![]() 更科学合理,试求
更科学合理,试求![]() 和
和![]() 的估计值(
的估计值(![]() 的结果精确到小数点后两位).
的结果精确到小数点后两位).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
,![]() 的值;
的值;
(2)若函数![]() 在
在![]() 和
和![]() 两处取得极值,求实数
两处取得极值,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下:

等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 | a | 24 | b |
(1)由该题中频率分布直方图求测试成绩的平均数和中位数;
(2)其他条件不变在评定等级为“合格”的学生中依次抽取2人进行座谈,每次抽取1人,求在第1次抽取的测试得分低于80分的前提下,第2次抽取的测试得分仍低于80分的概率;
(3)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2010年至2018年之间,受益于基础设施建设对光纤产品的需求,以及个人计算机及智能手机的下一代规格升级,电动汽车及物联网等新机遇,全球连接器行业增长呈现加速状态.根据如下折线图,下列结论正确的个数为( )
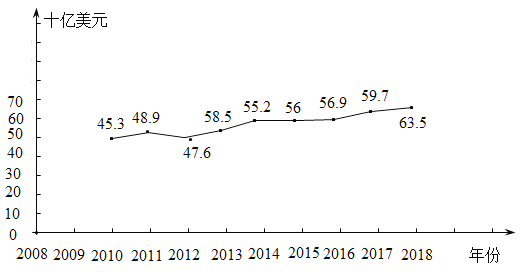
①每年市场规模逐年增加;
②市场规模增长最快的是2013年至2014年;
③这8年的市场规模增长率约为40%;
④2014年至2018年每年的市场规模相对于2010年至2014年每年的市场规模,数据方差更小,变化比较平稳.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,
时,
①若曲线![]() 与直线
与直线![]() 相切,求c的值;
相切,求c的值;
②若曲线![]() 与直线
与直线![]() 有公共点,求c的取值范围.
有公共点,求c的取值范围.
(2)当![]() 时,不等式
时,不等式![]() 对于任意正实数x恒成立,当c取得最大值时,求a,b的值.
对于任意正实数x恒成立,当c取得最大值时,求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com