
 (2013•宁德模拟)如图(1),在直角梯形 ABCD 中,AB∥CD,∠C=90°,CD=2AB=2,∠D=60°,E为DC中点,将四边形ABCE绕直线AE旋转90°得到四边形AB′C′E,
(2013•宁德模拟)如图(1),在直角梯形 ABCD 中,AB∥CD,∠C=90°,CD=2AB=2,∠D=60°,E为DC中点,将四边形ABCE绕直线AE旋转90°得到四边形AB′C′E,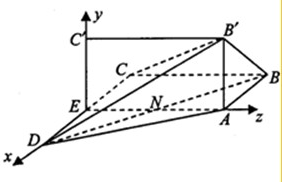 解:(Ⅰ)证明:∵CD=CD=2AB=2,∴CE=AB,又AB∥CD,且∠C=90°,∴四边形ABCD为矩形.∴AB⊥EA,EA⊥AB′,又AB∩B′=A,∴EA⊥平面ABB′,
解:(Ⅰ)证明:∵CD=CD=2AB=2,∴CE=AB,又AB∥CD,且∠C=90°,∴四边形ABCD为矩形.∴AB⊥EA,EA⊥AB′,又AB∩B′=A,∴EA⊥平面ABB′,| 3 |
| DB′ |
| 3 |
| DC |
| m |
|
|
| m |
| 3 |
| n |
| m |
| n |
| ||||
|
|
| 1 |
| 2 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•宁德模拟)某社区以“周末你最喜爱的一个活动”为题,对该社区2000个居民进行随机抽样调查(每位被调查居民必须而且只能从运动、上网、看书、聚会、其它等五项中选择一个项目)若抽取的样本容量为50,相应的条形统计图如图所示.据此可估计该社区中最喜欢运动的居民人数为( )
(2013•宁德模拟)某社区以“周末你最喜爱的一个活动”为题,对该社区2000个居民进行随机抽样调查(每位被调查居民必须而且只能从运动、上网、看书、聚会、其它等五项中选择一个项目)若抽取的样本容量为50,相应的条形统计图如图所示.据此可估计该社区中最喜欢运动的居民人数为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com