分析:(1)求出f′(x),因为x=1是函数的极值点,所以得到f'(1)=0求出m与n的关系式;
(2)令f′(x)=0求出函数的极值点,讨论函数的增减性确定函数的单调区间;
(3)构造函数h(x)=)=(
x
2ge
x-
x
3-x
2)-(
x
3-x
2)=x
2g(e
x-1-x),求导数,分类讨论,确定函数的单调性,即可得到结论.
解答:解:(1)f′(x)=3mx
2-6(m+1)x+n.
因为x=1是f(x)的一个极值点,所以f'(1)=0,即3m-6(m+1)+n=0.
所以n=3m+6;…(3分)
(2)由(1)知,f′(x)=3mx
2-6(m+1)x+3m+6=3m(x-1)[x-(1+
)]…(5分)
当m<0时,有1>1+
,当x变化时,f(x)与f'(x)的变化如下表:
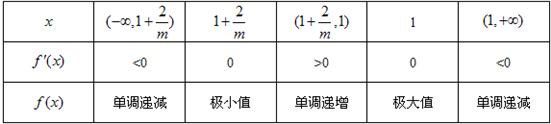
由上表知,当m<0时,f(x)在(-∞,1+
)单调递减,在(1+
,1)单调递增,在(1,+∞)单调递减
同理可得:当m>0时,f(x)在(-∞,1)单调递增,在(1,1+
)单调递减,在(1+
,+∞)上单调递增.…(9分)
(3)设函数h(x)=)=(
x
2ge
x-
x
3-x
2)-(
x
3-x
2)=x
2g(e
x-1-x)
由x
2≥0,且(e
x-1-x)′=e
x-1-1,故x≥1,(e
x-1-x)′=e
x-1-1≥0
令m(x)=e
x-1-x,所以m(x)在x≥1为增函数,故m(x)≥m(1)≥0
所以h(x)在[1,+∞),h(x)≥0,故g(x)≥φ(x)
当x<1,(e
x-1-x)′=e
x-1-1<0
令m(x)=e
x-1-x,所以m(x)在x<1为减函数,故m(x)<m(1)<0
所以h(x)在[1,+∞),h(x)<0,故g(x)<φ(x)
综上,x≥1时,g(x)≥φ(x),x<1时,g(x)<φ(x) …(14分)



