
| A. | 3个 | B. | 2个 | C. | 0个 | D. | 4个 |
分析 函数y=f[f(x)]-1的图象与x轴的交点个数即为f[f(x)]-1=0的解得个数,根据函数解析式的特点解得即可,
解答 解:y=f[f(x)]-1=0,
即f[f(x)]=1,
当f(x)+1=1时,即f(x)=0时,此时log2x=0,解得x=1,或x+1=0,解得x=-1,
当log2f(x)=1时,即f(x)=2时,此时x+1=2,解得x=1(舍去),或log2x=2,解得x=4,
综上所述函数y=f[f(x)]-1的图象与x轴的交点个数为3个,
故选:A.
点评 此题考查的是函数于函数图象交点个数的问题.在解答的过程当中充分体现了函数与方程的思想、问题转化的思想.值得同学们体会反思.


科目:高中数学 来源: 题型:选择题
| A. | a<b<c<d | B. | a<c<d<b | C. | b<a<c<d | D. | b<a<d<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n⊥β且α⊥β,则m∥n | B. | 若m∥α,n⊥α,则m⊥n | ||
| C. | 若m∥α,n∥β且α∥β,则m∥n | D. | 若α⊥β,α∩β=n,n⊥m⇒n⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21010-1 | B. | 21010-3 | C. | 3•21008-1 | D. | 21009-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | a<$\frac{1}{2}$ | C. | $\frac{1}{2}$<a<1 | D. | $\frac{1}{2}$≤a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
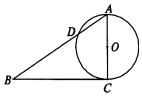 如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则$\frac{BD}{DA}$=( )
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则$\frac{BD}{DA}$=( )| A. | $\frac{16}{9}$ | B. | $\frac{25}{9}$ | C. | $\frac{25}{16}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com