
【题目】将函数y=sin(x+ ![]() )图象上各点的横坐标缩短到原来的
)图象上各点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),再向右平移
倍(纵坐标不变),再向右平移 ![]() 个单位,那么所得图象的一条对称轴方程为( )
个单位,那么所得图象的一条对称轴方程为( )
A.x=﹣ ![]()
B.x=﹣ ![]()
C.x= ![]()
D.x= ![]()
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的函数,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式exf(x)>ex+1的解集为( )
A.(0,+∞)
B.(﹣∞,0)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣∞,﹣1)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a. 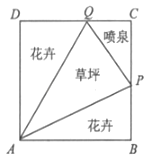
(1)当∠PAQ= ![]() 时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
(2)考虑到小区道路的整体规划,要求PB+DQ=PQ,请探究∠PAQ是否为定值,若是,求出此定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个匀速旋转的摩天轮每12分钟转一周,最低点距地面2米,最高点距地面18米,P是摩天轮轮周上一定点,从P在最低点时开始计时,则14分钟后P点距地面的高度是米.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4sin2( ![]() +
+ ![]() )sinx+(cosx+sinx)(cosx﹣sinx)﹣1.
)sinx+(cosx+sinx)(cosx﹣sinx)﹣1.
(1)化简f(x);
(2)常数ω>0,若函数y=f(ωx)在区间 ![]() 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围;
(3)若函数g(x)= ![]() 在
在 ![]() 的最大值为2,求实数a的值.
的最大值为2,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() =1,点M与曲线C的焦点不重合,若点M关于曲线C的两个焦点的对称点分别为A,B,M,N是坐标平面内的两点,且线段MN的中点P恰好在双曲线C上,则|AN﹣BN|= .
=1,点M与曲线C的焦点不重合,若点M关于曲线C的两个焦点的对称点分别为A,B,M,N是坐标平面内的两点,且线段MN的中点P恰好在双曲线C上,则|AN﹣BN|= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点M(1,1),且与x轴,y轴的正半轴分别相交于A,B两点,O为坐标原点.求:
(1)当|OA|十|OB|取得最小值时,直线l的方程;
(2)当|MA|2+|MB|2取得最小值时,直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数f(x)与g(x)的图象相同的是( )
A.f(x)=x,g(x)=( ![]() )2
)2
B.f(x)=x2 , g(x)=(x+1)2
C.f(x)=1,g(x)=x0
D.f(x)=|x|,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆E:(x+ ![]() )2+y2=16,点F(
)2+y2=16,点F( ![]() ,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q. 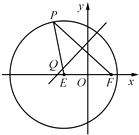
(1)求动点Q的轨迹Γ的方程;
(2)设直线l与(1)中轨迹Γ相交于A,B两点,直线AO,l,OB的斜率分别为k1 , k,k2(其中k>0),若k1 , k,k2恰好构成公比不为1的等比数列,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com