
【题目】如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以Z表示.
(1)如果Z=8,求乙组同学植树棵数的平均数和方差;
(2)如果Z=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
【答案】
(1)解:当Z=8时,由茎叶图知,
乙组同学的植树棵数是8,8,9,10,
∴ ![]() =
= ![]() ,
,
![]() [(8﹣
[(8﹣ ![]() )2+(8﹣
)2+(8﹣ ![]() )2+(9﹣
)2+(9﹣ ![]() )2+(10﹣
)2+(10﹣ ![]() )2]=
)2]= ![]()
(2)解:Z=9时,甲组四名同学植树棵数分别为9,9,11,11,
乙组四名同学植树棵数分别为9,8,9,10,
分别从甲、乙两组中随机取一名同学,
所有可能结果n=4×4=16,
选出这两名同学的植树总棵数为19,包含基本事件个数m=4,
∴这两名同学的植树总棵数为19的概率:
p= ![]() .
.
【解析】(1)当Z=8时,由茎叶图知,乙组同学的植树棵数是8,8,9,10,由此能求出乙组同学植树棵数的平均数和方差.(2)Z=9时,甲组四名同学植树棵数分别为9,9,11,11,乙组四名同学植树棵数分别为9,8,9,10,分别从甲、乙两组中随机取一名同学,所有可能结果n=4×4=16,选出这两名同学的植树总棵数为19,包含基本事件个数m=4,由此能求出这两名同学的植树总棵数为19的概率.
【考点精析】关于本题考查的茎叶图,需要了解茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() , 其中左焦点F(﹣2,0).
, 其中左焦点F(﹣2,0).
(1)求椭圆C的方程;
(2)若直线y=x+m与椭圆C交于不同的两点A,B,且线段的中点M在圆x2+y2=1上,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为2正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C,有如下四个判断:
①AC⊥BD
②AB与平面BCD所成60°角
③△ABC是等边三角形
④若A、B、C、D四点在同一个球面上,则该球的表面积为8π
其中正确判断的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是绵阳市某小区100户居民2014年平均用水量(单位:t)的频率分布直方图,则该小区2014年的月平均用水量的众数,中位数的估计值分别是( ) 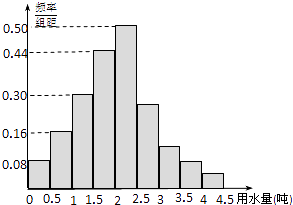
A.2,2.5
B.2,2.02
C.2.25,2.5
D.2.25,2.02
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(1,0,﹣1),平行于向量![]() =(2,1,1),平面α过直线l与点M(1,2,3),则平面α的法向量不可能是( )
=(2,1,1),平面α过直线l与点M(1,2,3),则平面α的法向量不可能是( )
A.(1,﹣4,2)
B.(![]() ,-1,
,-1,![]() )
)
C.(-![]() ,1,-
,1,-![]() )
)
D.(0,﹣1,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com