
关于 的函数
的函数 ,有下列结论:
,有下列结论:
①、该函数的定义域是 ; ②、该函数是奇函数;
; ②、该函数是奇函数;
③、该函数的最小值为 ;
;
④、当 时
时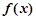 为增函数,当
为增函数,当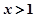 时
时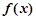 为减函数;
为减函数;
其中,所有正确结论的序号是 。
①④
解析试题分析: :①函数f(x)的定义域是(0,+∞),令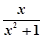 >0,解得x>0,故定义域是(0,+∞),命题正确;
>0,解得x>0,故定义域是(0,+∞),命题正确;
②函数f(x)是奇函数,由①知,定义域不关于原点对称,故不是奇函数,命题不正确;
③函数f(x)的最大值为-lg2,因为f(x)= 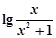 =lg
=lg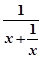 ≤lg
≤lg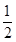 =-lg2,最大值是-lg2,故命题不正确;
=-lg2,最大值是-lg2,故命题不正确;
④当0<x<1时,函数f(x)是增函数;当x>1时,函数f(x)是减函数,命题正确,因为f′(x)=lg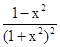 ,令导数大于0,可解得0<x<1,令导数大于0,得x>1,故命题正确.综上,①④正确,故答案为:①④
,令导数大于0,可解得0<x<1,令导数大于0,得x>1,故命题正确.综上,①④正确,故答案为:①④
考点:本题主要考查了函数定义域、最值、单调性和奇偶性,同时考查了推理论证的能力以及计算论证的能力,属于中档题.
点评:解决该试题的关键是①根据对数函数的真数大于0,建立关系式解之验证定义域即可;②函数f(x)是奇函数,利用奇函数的定义进行判断;③函数f(x)的最大值为-lg2,利用基本不等式与对数的运算性质求出最值;④求出导数,解出单调区间,验证即可.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
某同学在研究函数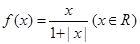 时,分别给出下面几个结论:
时,分别给出下面几个结论:
①等式 对
对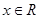 恒成立; ②函数
恒成立; ②函数 的值域为
的值域为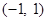 ;
;
③若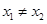 ,则一定有
,则一定有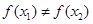 ; ④函数
; ④函数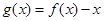 在
在 上有三个零点。 其中正确结论的序号有____________.
上有三个零点。 其中正确结论的序号有____________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列5个判断:
①若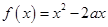 在
在 上增函数,则
上增函数,则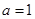 ;
;
②函数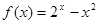 只有两个零点;
只有两个零点;
③函数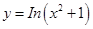 的值域是
的值域是 ;
;
④函数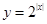 的最小值是1;
的最小值是1;
⑤在同一坐标系中函数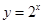 与
与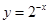 的图像关于
的图像关于 轴对称。
轴对称。
其中正确命题的序号是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com