
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为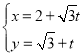 (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为
轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程及曲线C的直角坐标方程;
的极坐标方程及曲线C的直角坐标方程;
(2)若![]() 是直线
是直线![]() 上的一点,
上的一点,![]() 是曲线C上的一点,求
是曲线C上的一点,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() 是
是![]() 的一个三等分点(靠近点
的一个三等分点(靠近点![]() ),
),![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.

(1)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某飞机失联,经卫星侦查,其最后出现在小岛![]() 附近,现派出四艘搜救船
附近,现派出四艘搜救船![]() ,为方便联络,船
,为方便联络,船![]() 始终在以小岛
始终在以小岛![]() 为圆心,100海里为半径的圆上,船
为圆心,100海里为半径的圆上,船![]() 构成正方形编队展开搜索,小岛
构成正方形编队展开搜索,小岛![]() 在正方形编队外(如图).设小岛
在正方形编队外(如图).设小岛![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() ,
,![]() 船到小岛
船到小岛![]() 的距离为
的距离为![]() .
.
(1)请分别求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并分别写出定义域;
,并分别写出定义域;
(2)当![]() 两艘船之间的距离是多少时搜救范围最大(即
两艘船之间的距离是多少时搜救范围最大(即![]() 最大)?
最大)?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,直线l过点
,直线l过点![]() 且与x轴不重合,l交圆
且与x轴不重合,l交圆![]() 于C,D两点,过
于C,D两点,过![]() 作
作![]() 的平行线,交
的平行线,交![]() 于点E.设点E的轨迹为
于点E.设点E的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 相切于点M,
相切于点M,![]() 与两坐标轴的交点为A与B,直线
与两坐标轴的交点为A与B,直线![]() 经过点M且与
经过点M且与![]() 垂直,
垂直,![]() 与
与![]() 的另一个交点为N,当
的另一个交点为N,当![]() 取得最小值时,求
取得最小值时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() ,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)在平面直角坐标系xOy中,A(﹣2,0),B(0,﹣2),M是曲线C上任意一点,求△ABM面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的方程为
的方程为![]() ,
,![]() 的方程为
的方程为![]() ,
,![]() 是一条经过原点且斜率大于
是一条经过原点且斜率大于![]() 的直线.
的直线.
(1)以直角坐标系原点![]() 为极点,
为极点,![]() 轴正方向为极轴建立极坐标系,求
轴正方向为极轴建立极坐标系,求![]() 与
与![]() 的极坐标方程;
的极坐标方程;
(2)若![]() 与
与![]() 的一个公共点
的一个公共点![]() (异于点
(异于点![]() ),
),![]() 与
与![]() 的一个公共点为
的一个公共点为![]() ,当
,当![]() 时,求
时,求![]() 的直角坐标方程.
的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,若![]() 是函数
是函数![]() 的零点,且
的零点,且![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,函数
时,函数![]() 有两个零点
有两个零点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的函数![]() ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数![]() 使得
使得![]() 对任意实数x都成立,则称
对任意实数x都成立,则称![]() 是一个“k~特征函数”.则下列结论中正确命题序号为____________.
是一个“k~特征函数”.则下列结论中正确命题序号为____________.
①![]() 是一个“k~特征函数”;②
是一个“k~特征函数”;②![]() 不是“k~特征函数”;
不是“k~特征函数”;
③![]() 是常数函数中唯一的“k~特征函数”;④“
是常数函数中唯一的“k~特征函数”;④“![]() ~特征函数”至少有一个零点;
~特征函数”至少有一个零点;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com