
【题目】如图所示,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.
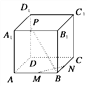
(1)若![]() ,求证:无论点P在DD1上如何移动,总有BP⊥MN;
,求证:无论点P在DD1上如何移动,总有BP⊥MN;
(2)棱DD1上是否存在这样的点P,使得平面APC1⊥平面ACC1?证明你的结论.
【答案】(1)证明见解析;(1)存在点P,证明见解析;
【解析】解:(1)证明:连AC,BD,在△ABC中,
∵=,∴MN∥AC.
又∵AC⊥BD,DD1⊥底面ABCD.
∴DD1⊥AC,故AC⊥平面BDD1B1.
进而MN⊥平面BDD1B1,
∵BP面BDD1B1,
∴MN⊥BP.
(2)假设存在点P,使面APC1⊥面ACC1,过P作PF⊥AC1,则PF⊥面ACC1.
又∵BD⊥面ACC1,∴PF∥BD,而两平行线PF、BD所确定的平面即为两相交直线BD、DD1确定的对角面BB1D1D,
∴F为AC1与对角面BB1D1D的交点,
故F为AC1的中点,由PF∥BD,P∈DD1知,P也是DD1的中点.
显然,当P为DD1中点,F为AC1中点时,
∵AP=PC1,∴PF⊥AC1
又PF∥BD,BD⊥AC,∴PF⊥AC.
从而PF⊥面ACC1,则面APC1⊥面ACC1.
故存在点P,使P为DD1中点时,面APC1⊥面ACC1.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求![]() 的值;(2)求
的值;(2)求![]() 的单调区间;
的单调区间;
(3)设![]() (其中
(其中![]() 为
为![]() 的导函数)。证明:对任意
的导函数)。证明:对任意![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(数学文卷·2017届北京市朝阳区高三上学期期中考试第14题) 《九章算术》是我国古代一部重要的数学著作.书中有如下问题:“今有良马与驽马发长安,至齐。齐去长安三千里,良马初日行一百九十三里,日增一十三里;驽马初日行九十七里,日减半里.良马先至齐,复还迎驽马.问几何日相逢.”其意为:“现在有良马和驽马同时从长安出发到齐去.已知长安和齐的距离是3000里,良马第一天行193里,之后每天比前一天多行13里;驽马第一天行97里,之后每天比前一天少行0.5里.良马到齐后,返回去迎驽马.多少天后两马相遇.”利用我们所学的知识,可知离开长安后的第______天,两马相逢.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点.

(1)求证:直线MF∥平面ABCD;
(2)求证:平面AFC1⊥平面ACC1A1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】信息科技的进步和互联网商业模式的兴起,全方位地改变了大家金融消费的习惯和金融交易模式,现在银行的大部分业务都可以通过智能终端设备完成,多家银行职员人数在悄然减少.某银行现有职员320人,平均每人每年可创利20万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.2万元,但银行需付下岗职员每人每年6万元的生活费,并且该银行正常运转所需人数不得小于现有职员的![]() ,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续![]() 天监测空气质量指数
天监测空气质量指数![]() ,数据统计如下:
,数据统计如下:

(Ⅰ)根据所给统计表和频率分布直方图中的信息求出![]() 、
、![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
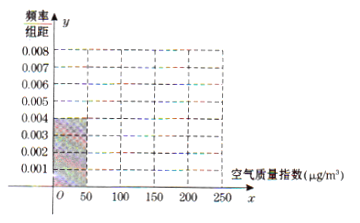
(Ⅱ)在空气质量指数分别为![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件
的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有编号分别为1,2,3,…,2n的![]() 个小球,现将袋中的小球分给
个小球,现将袋中的小球分给![]() 三个盒子,每次从袋中任意取出两个小球,将其中一个放入A盒子,如果这个小球的编号是奇数,就将另一个放入
三个盒子,每次从袋中任意取出两个小球,将其中一个放入A盒子,如果这个小球的编号是奇数,就将另一个放入![]() 盒子,否则就放入
盒子,否则就放入![]() 盒子,重复上述操作,直到所有小球都被放入盒中,则下列说法一定正确的是
盒子,重复上述操作,直到所有小球都被放入盒中,则下列说法一定正确的是
A. ![]() 盒中编号为奇数的小球与
盒中编号为奇数的小球与![]() 盒中编号为偶数的小球一样多
盒中编号为偶数的小球一样多
B. ![]() 盒中编号为偶数的小球不多于
盒中编号为偶数的小球不多于![]() 盒中编号为偶数的小球
盒中编号为偶数的小球
C. ![]() 盒中编号为偶数的小球与C盒中编号为奇数的小球一样多
盒中编号为偶数的小球与C盒中编号为奇数的小球一样多
D. B盒中编号为奇数的小球多于C盒中编号为奇数的小球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com