
����Ŀ����ͼ�����ߦ�������C1�� ![]() ��a��b��0��y��0��������C2��
��a��b��0��y��0��������C2�� ![]() ��a��0��b��0��y��0����ɣ����е�F1 �� F2Ϊ����C1����Բ���ߵĽ��㣬��F3 �� F4Ϊ����C2����Բ���ߵĽ��㣬
��a��0��b��0��y��0����ɣ����е�F1 �� F2Ϊ����C1����Բ���ߵĽ��㣬��F3 �� F4Ϊ����C2����Բ���ߵĽ��㣬
������F2��2��0����F3����6��0���������ߦ��ķ��̣�
������ͼ����ֱ��lƽ��������C2�Ľ����ߣ�������C1�ڵ�A��B����֤����AB���е�M��������C2����һ���������ϣ�
�����ڣ����е����ߦ�����ֱ��l1����F4������C1�ڵ�C��D�����CDF1��������ֵ��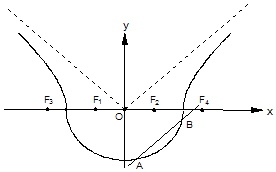
���𰸡��⣺����F2��2��0����F3����6��0������ 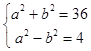 a
a 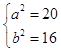 �����ߦ��ķ���Ϊ
�����ߦ��ķ���Ϊ ![]() ��
�� ![]() ��y��0��
��y��0��
��������C2�Ľ�����Ϊy=�� ![]() ����ͼ����ֱ��l��y=
����ͼ����ֱ��l��y= ![]()
�� 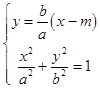 2x2��2mx+��m2��a2��=0
2x2��2mx+��m2��a2��=0
��=��2m��2��42��m2��a2��=8a2��4m2��0�� ![]()
�������ν��֪m��a�� ![]()
���A��x1 �� y1����B��x2 �� y2����M��x0 �� y0���� 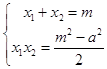 ��
��
�� ![]() ��
�� ![]()
�� ![]() ������M��ֱ��y=��
������M��ֱ��y=�� ![]() �ϣ�
�ϣ�
�����ɣ���֪������C1Ϊ ![]() ����F4��6��0����
����F4��6��0����
��ֱ��l1�ķ���Ϊx=ny+6��n��0��
�� 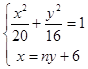 ��4n2+5��y2+48ny+64=0
��4n2+5��y2+48ny+64=0
��=��48n��2��4��64��4n2+5����0n2��1
��C��x3 �� y3����D��x4 �� y4����Τ�ﶨ���� 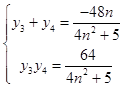
|y3��y4|= ![]() ��
��
s��CDF1= ![]() |F1F4|��|y3��y4|=
|F1F4|��|y3��y4|= ![]()
��t= ![]() ����n2=t2+1��s��CDF1=64
����n2=t2+1��s��CDF1=64 ![]() ��
�� 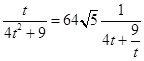
��t��0���� ![]() �����ҽ���t=
�����ҽ���t= ![]() ��n=
��n= ![]() ʱ�Ⱥų���
ʱ�Ⱥų���
��n= ![]() ʱ����CDF1��������ֵ
ʱ����CDF1��������ֵ ![]()
��������������F2��2��0����F3����6��0�����ɵã� ![]() a��������C2�Ľ�����Ϊ��
a��������C2�Ľ�����Ϊ�� ![]() ����ͼ�����A��x1 �� y1����B��x2 �� y2����M��x0 �� y0������ֱ��l��y=
����ͼ�����A��x1 �� y1����B��x2 �� y2����M��x0 �� y0������ֱ��l��y= ![]() ������Բ����������Ϊ2x2��2mx+��m2��a2��=0�����á���0������ϵ���Ĺ�ϵ���е����깫ʽ��ֻҪ֤��y0=��
������Բ����������Ϊ2x2��2mx+��m2��a2��=0�����á���0������ϵ���Ĺ�ϵ���е����깫ʽ��ֻҪ֤��y0=�� ![]() ���ɣ�������ֱ��l1�ķ���Ϊx=ny+6��n��0��������Բ���������ɵã�5+4n2��y2+48ny+64=0�����ø���ϵ���Ĺ�ϵ���ҳ���ʽ�������ε�������㹫ʽ����������ʽ�����ʼ��ɵó���
���ɣ�������ֱ��l1�ķ���Ϊx=ny+6��n��0��������Բ���������ɵã�5+4n2��y2+48ny+64=0�����ø���ϵ���Ĺ�ϵ���ҳ���ʽ�������ε�������㹫ʽ����������ʽ�����ʼ��ɵó���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=sin��x+ ![]() ��+sin��x��
��+sin��x�� ![]() ��+cosx+a��a��R��a�dz�������
��+cosx+a��a��R��a�dz�������
��1������f��x������С�����ڣ�
��2����a=0������y=f��x����[���У���]�ϵ�ͼ��
��3����x��[�� ![]() ��
�� ![]() ]ʱ��f��x�������ֵΪ1����a��ֵ��
]ʱ��f��x�������ֵΪ1����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������У������ȡ100�����������������λ���ˣ����ݰ�������![]() ��
��![]() ��
��![]() ��
��![]() ���з��飬�õ����ʷֲ�ֱ��ͼ����ͼ��ʾ.
���з��飬�õ����ʷֲ�ֱ��ͼ����ͼ��ʾ.
��1������Ƶ�ʷֲ�ֱ��ͼ�����ȡ��100�����ӵ����������Ĺ���ֵ.
��2���÷ֲ�����ķ�����������![]() ��
��![]() �������й���ȡ5��������������
�������й���ȡ5��������������![]() ���м�����
�������
��3���ڣ�2���г����5�������У���ȡ2�ˣ���������![]() �����������1���ĸ���.
�����������1���ĸ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��
��![]() ��
��![]() �գ������ʽ�����Ϣ����ᡱ��ɽ���ൺ��Ļ.Ϊ�˽���Щ�˸���ע�����ʽ�����Ϣ����ᡱ��ij���������ȡ��������
�գ������ʽ�����Ϣ����ᡱ��ɽ���ൺ��Ļ.Ϊ�˽���Щ�˸���ע�����ʽ�����Ϣ����ᡱ��ij���������ȡ��������![]() -
-![]() ��֮���
��֮���![]() �˽��е��飬����������Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ�����������Ϊ��
�˽��е��飬����������Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ�����������Ϊ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .��������������
.��������������![]() ��
��![]() �ڵ��˷ֱ��Ϊ�������ꡱ�͡������ꡱ.
�ڵ��˷ֱ��Ϊ�������ꡱ�͡������ꡱ.

��ע | ����ע | �ϼ� | |
������ |
| ||
������ | |||
�ϼ� |
|
|
|
��1������Ƶ�ʷֲ�ֱ��ͼ����������λ����������λС������������
��2��������֪�������![]() �����������ж��ܷ���
�����������ж��ܷ���![]() �İ�����Ϊ�������ꡱ�ȡ������ꡱ���ӹ�ע�����ʽ�����Ϣ����ᡱ��
�İ�����Ϊ�������ꡱ�ȡ������ꡱ���ӹ�ע�����ʽ�����Ϣ����ᡱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() ��
��![]() ����Ȼ�����ĵ�����.
����Ȼ�����ĵ�����.
��1������![]() �ĵ������䣻
�ĵ������䣻
��2����![]() ����
����![]() ʱ������
ʱ������![]() �����ֵ��
�����ֵ��
��3����![]() ����
����![]() ���Ƚϣ�
���Ƚϣ�![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn �� ������4nSn=��n+1��2an��n��N*����a1=1
������an��
������bn= ![]() ������{bn}��ǰn���ΪTn �� ��֤��Tn
������{bn}��ǰn���ΪTn �� ��֤��Tn ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������������ABCA1B1C1�У�AB=2��AA1=2���ɶ���B����������(������AA1)���ﶥ��C1����AA1�Ľ����ΪM.��
(1)����������չ��ͼ�ĶԽ��߳���
(2)��B��M��C1�����·�߳�����ʱ![]() ��ֵ.
��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c��a=b��sinC+cosC����
�������ABC��
��������A= ![]() ��DΪ��ABC��һ�㣬DB=2��DC=1�����ı���ABDC��������ֵ��
��DΪ��ABC��һ�㣬DB=2��DC=1�����ı���ABDC��������ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com