
【题目】已知中心在坐标原点O,焦点在x轴上,离心率为![]() 的椭圆过点
的椭圆过点![]() .
.
(1)求椭圆的方程;
(2)设不过原点O的直线l与该椭圆交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,若![]() 的面积为
的面积为![]() ,求直线l与y轴交点的坐标.
,求直线l与y轴交点的坐标.
【答案】(1)![]() ;(2)
;(2)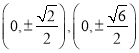
【解析】
(1)设出椭圆的方程,将已知点代入椭圆的方程及利用椭圆的离心率公式得到关于椭圆的三个参数的等式,解方程组求出![]() 的值,代入椭圆方程即可.(2)设出直线的方程将直线方程与椭圆方程联立,消去
的值,代入椭圆方程即可.(2)设出直线的方程将直线方程与椭圆方程联立,消去![]() 得到关于
得到关于![]() 的二次方程,利用韦达定理得到关于两个交点的坐标的关系,将直线
的二次方程,利用韦达定理得到关于两个交点的坐标的关系,将直线![]() 的斜率用坐标表示据已知三个斜率成等比数列,列出方程,将韦达定理得到的等式代入,求出
的斜率用坐标表示据已知三个斜率成等比数列,列出方程,将韦达定理得到的等式代入,求出![]() 的值,利用判别式大于
的值,利用判别式大于![]() 得到
得到![]() 的范围,将
的范围,将![]() 面积表示出来,得到
面积表示出来,得到![]() 的等式,解出
的等式,解出![]() ,即可得到直线l与y轴交点的坐标.
,即可得到直线l与y轴交点的坐标.
(1)设椭圆方程为:![]() ,
,
椭圆的离心率为![]() ,过点
,过点![]() ,
,
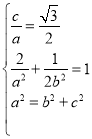 ,解得
,解得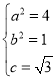 ,
,
![]() 椭圆的方程为:
椭圆的方程为:![]() .
.
(2)由题意知,直线![]() 的斜率存在且不为0,
的斜率存在且不为0,
设直线![]() 的方程为:
的方程为:![]() ,
,
![]()
![]() ,消
,消![]() 得,
得,![]() ,
,
![]()
且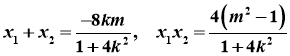 ,
,
![]() ,
,
![]() 直线
直线![]() 的斜率依次成等比数列,
的斜率依次成等比数列,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,即
,即![]() ,
,
![]() 直线
直线![]() 的斜率存在,且
的斜率存在,且![]() ,得
,得![]() 且
且![]() .
.
设![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离,
![]()
![]()
![]()
![]() 或
或![]() ,
,
![]() 直线
直线![]() 与
与![]() 轴交点的坐标为:
轴交点的坐标为: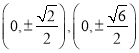 .
.


科目:高中数学 来源: 题型:
【题目】如图a是某市参加2012年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为![]() 、
、![]() 、…、
、…、![]() [如
[如![]() 表示身高(单位:cm)在
表示身高(单位:cm)在![]() 内的学生人数].图b是统计图a中身高在一定范围内学生人数的一个算法流程图.现要统计身高在
内的学生人数].图b是统计图a中身高在一定范围内学生人数的一个算法流程图.现要统计身高在![]() (含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是( )
(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线C:![]() 的焦点为F,过F的直线
的焦点为F,过F的直线![]() 交抛物线C于A,B两点.
交抛物线C于A,B两点.
(1)求线段AF的中点M的轨迹方程;
(2)已知△AOB的面积是△BOF面积的3倍,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】销售甲、乙两种商品所得利润分别是![]() 万元,它们与投入资金
万元,它们与投入资金![]() 万元的关系分别为
万元的关系分别为![]() ,
,![]() ,(其中
,(其中![]() 都为常数),函数
都为常数),函数![]() 对应的曲线
对应的曲线![]() 、
、![]() 如图所示.
如图所示.

(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)若该商场一共投资4万元经销甲、乙两种商品,求该商场所获利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以椭圆
,且以椭圆![]() 的两焦点和短轴的一个端点为顶点的三角形的周长恰为
的两焦点和短轴的一个端点为顶点的三角形的周长恰为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)动直线![]() 与抛椭圆
与抛椭圆![]() 相交于
相交于![]() ,
,![]() 两点,问:在
两点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() (其中
(其中![]() ,使得向量
,使得向量![]() 与向量
与向量![]() 共线(其中
共线(其中![]() 为坐标原点)?若存在,求出点
为坐标原点)?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市食品药品监督管理局开展2020年春季快递餐饮安全检查,对本市的8个快递配餐点进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如表所示:
快递配餐点编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分 | 82 | 75 | 70 | 66 | 83 | 93 | 95 | 100 |
卫生标准评分 | 81 | 79 | 77 | 75 | 82 | 83 | 84 | 87 |
(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(精确到0.1)
的线性回归方程;(精确到0.1)
(2)现从8个被检查点中任意抽取两个组成一组,若两个点的原料采购加工标准和卫生标准的评分均超过80分,则组成“快递标兵配餐点”,求该组被评为“快递标兵配餐点”的概率.
参考公式: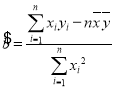 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() 个小球,甲、乙两位同学轮流且不放回抓球,每次最少抓1个球,最多抓3个球,规定谁抓到最后一个球谁赢. 如果甲先抓,那么下列推断正确的是( )
个小球,甲、乙两位同学轮流且不放回抓球,每次最少抓1个球,最多抓3个球,规定谁抓到最后一个球谁赢. 如果甲先抓,那么下列推断正确的是( )
A. 若![]() =4,则甲有必赢的策略 B. 若
=4,则甲有必赢的策略 B. 若![]() =6,则乙有必赢的策略
=6,则乙有必赢的策略
C. 若![]() =9,则甲有必赢的策略 D. 若
=9,则甲有必赢的策略 D. 若![]() =11,则乙有必赢的策略
=11,则乙有必赢的策略
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com