考点:二面角的平面角及求法,棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)设AD的中点为N,连结ON,确定A
1N为B
1O在平面ADD
1A
1内的射影,证明Rt△A
1AN≌Rt△ADM,即可证明异面直线B
1O与AM垂直;
(Ⅱ)利用面积比,求二面角B
1-AM-B的大小;
(Ⅲ)由(Ⅰ)知,B
1O⊥平面AMC.所以V
B1-AMC=
B
1O×S
△AMC,即可求三棱锥B
1-AMC的体积.
解答:
(Ⅰ)证明:设AD的中点为N,连结ON,
由O为正方形ABCD的中心,得ON⊥平面ADD
1A
1.
又AA
1⊥平面ADD
1A
1,所以A
1N为B
1O在平面ADD
1A
1内的射影.
在正方形ADD
1A
1中,Rt△A
1AN≌Rt△ADM,
∴∠AA
1N=∠MAD,
∴∠AA
1N+∠A
1AM=
,
∴A
1N⊥AM,
∴B
1O⊥AM;
(Ⅱ)解:设正方体的棱长为2,则AM=
,B
1A=2
,B
1M=3,∴cos∠MB
1A=
=
,
∴sin∠MB
1A=45°,
∴
S△AB1M=
×3×2×=3,
△AMB中,AM=
,BA=2,BM=3,∴S
△AMB=
×2×=
,
∴二面角B
1-AM-B的余弦值为
,
∴二面角B
1-AM-B的大小为arccos
;
(Ⅲ)解:由(Ⅰ)知,B
1O⊥平面AMC.所以V
B1-AMC=
B
1O×S
△AMC因棱长为a,所以B
1O=
a,S
△AMC=
×MO×AC=
a
a=
a
2故V
B1-AMC=
×
a×
a
2=
a
3.
点评:本题考查二面角的平面角及求法,考查棱柱、棱锥、棱台的体积,考查学生分析解决问题的能力,属于中档题.

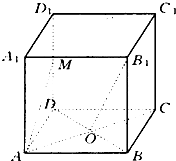 在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,M为D1D的中点.
在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,M为D1D的中点. 

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案