
【题目】12个朋友每周聚餐一次,每周他们分成三组,每组4人,不同组坐不同的桌子.若要求这些朋友中任意两个人至少有一次同坐一张桌子,则至少需要周____周.
【答案】5
【解析】
首先,就某个人而言,每周与另外3人坐在一起,则至少需要4周.其次,12个人两两配对共有![]() 对,每张桌子上有
对,每张桌子上有![]() 对,于是,第一周3×6=18对互相认识.
对,于是,第一周3×6=18对互相认识.
由于4人坐3桌,在第一周后的每一周,在每张桌子上肯定至少有两人在第一周已坐在一起,也就是新认识的对子最大数目是每周每桌有6-1=5(对),共计15对.
因为18+15+15+15=63,所以用4周是不可能两两有一次同坐一桌的,从而知需5击.用5周是可以办到的,例如,第一周18对,其余4击每周12对,共计18+12×4=66对,下面给出具体分桌方案:
周次 桌1 桌2 桌3
1 1 2 3 4 5 6 9 10 7 8 11 12
2 1 2 5 6 3 4 7 8 9 10 11 12
3 1 2 7 8 3 4 9 10 5 6 11 12
4 1 2 9 10 3 4 11 12 5 6 7 8
5 1 2 11 12 3 4 5 6 7 8 9 10


科目:高中数学 来源: 题型:
【题目】天干地支纪年法,源于中国,中国自古便有十天干与十二地支.十天干:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,之后地支回到“子”重新开始,即“丙子”,…,以此类推,已知2016年为丙申年,那么到改革开放100年时,即2078年为________年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于![]() .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的左顶点
的左顶点![]() 为圆心作圆
为圆心作圆![]() :
:![]() ,设圆
,设圆![]() 与椭圆
与椭圆![]() 交于点
交于点![]() 与点
与点![]() .
.
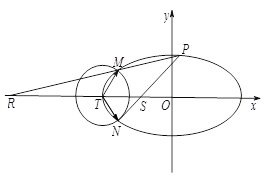
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的最小值,并求此时圆
的最小值,并求此时圆![]() 的方程;
的方程;
(3)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,且直线
的任意一点,且直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
,![]() 为坐标原点,
为坐标原点,
求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为了了解某日旅游鞋的销售情况,抽取了部分顾客所购鞋的尺寸,将所得数据整理后,画出频率分布直方图如图所示.已知从左到右前3个小组的频率之比为1∶2∶3,第4小组与第5小组的频率分布如图所示,第2小组的频数为10,则第4小组顾客的人数是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凸![]() 边形
边形![]() 玫瑰园的
玫瑰园的![]() 个顶点各栽有1棵红玫瑰,每两棵红玫瑰之间都有一条直小路想通,这些直小路没有出现“三线共点”的情况——它们把花园分割成许多不重叠的区域(三角形、四边形、……),每块区域都栽有一棵白玫瑰(或黑玫瑰).
个顶点各栽有1棵红玫瑰,每两棵红玫瑰之间都有一条直小路想通,这些直小路没有出现“三线共点”的情况——它们把花园分割成许多不重叠的区域(三角形、四边形、……),每块区域都栽有一棵白玫瑰(或黑玫瑰).
(1)求出玫瑰园里玫瑰总棵树![]() 的表达式.
的表达式.
(2)花园里能否恰有99棵玫瑰?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的内切圆
的内切圆![]() 切边
切边![]() 于点
于点![]() , 而
, 而![]() 是边
是边![]() 上的任意内点.设
上的任意内点.设![]() 和
和![]() 的内切圆圆心分别是
的内切圆圆心分别是![]() 和
和![]() .
.
(1)求证:∠I1DI2 =90°(即![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆);
四点共圆);
(2)设![]() 、
、![]() 、
、![]() 、
、![]() 四点所在的圆周的半径为
四点所在的圆周的半径为![]() , 而
, 而![]() 的内切圆半径为
的内切圆半径为![]() ,试求
,试求![]() 的取值范围(
的取值范围(![]() 取遍各种形状的三角形,点
取遍各种形状的三角形,点![]() 取遍边
取遍边![]() 上的每一个内点).
上的每一个内点).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com