
【题目】如图,已知抛物线![]() 的焦点是
的焦点是![]() ,准线是
,准线是![]() ,抛物线上任意一点
,抛物线上任意一点![]() 到
到![]() 轴的距离比到准线的距离少2.
轴的距离比到准线的距离少2.

(1)写出焦点![]() 的坐标和准线
的坐标和准线![]() 的方程;
的方程;
(2)已知点![]() ,若过点
,若过点![]() 的直线交抛物线
的直线交抛物线![]() 于不同的两点
于不同的两点![]() (均与
(均与![]() 不重合),直线
不重合),直线![]() 分别交
分别交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() 交于点
交于点![]() ,
,![]() 是
是![]() 上任意一点.
上任意一点.
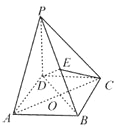
(1)求证![]() ;
;
(2)已知二面角![]() 的余弦值为
的余弦值为![]() ,若
,若![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,点
,点![]() 平面
平面![]() ,点
,点![]() 在平面
在平面![]() 的同侧,且
的同侧,且![]() 在平面
在平面![]() 上的射影分别为
上的射影分别为![]() ,
,![]() .
.
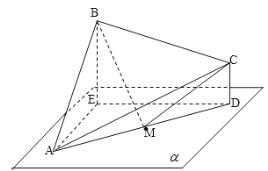
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 是
是![]() 中点,求平面
中点,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线C:y2=8x上一点A到焦点F的距离为6,若点P为抛物线C准线上的动点,则|OP|+|AP|的最小值为( )
A. 4B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点是
的焦点是![]() ,准线是
,准线是![]() ,抛物线上任意一点
,抛物线上任意一点![]() 到
到![]() 轴的距离比到准线的距离少2.
轴的距离比到准线的距离少2.

(1)写出焦点![]() 的坐标和准线
的坐标和准线![]() 的方程;
的方程;
(2)已知点![]() ,若过点
,若过点![]() 的直线交抛物线
的直线交抛物线![]() 于不同的两点
于不同的两点![]() (均与
(均与![]() 不重合),直线
不重合),直线![]() 分别交
分别交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程是
的参数方程是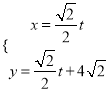 (
(![]() 是参数),以坐标原点为原点,
是参数),以坐标原点为原点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)过直线![]() 上的点作曲线
上的点作曲线![]() 的切线,求切线长的最小值.
的切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出,坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村真脱贫,坚持扶贫同扶智相结合,帮助贫困村种植蜜柚,并利用电商进行销售,为了更好地销售,现从该村的蜜柚树上随机摘下了100个蜜柚进行测重,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,其频率分布直方图如图所示.
(单位:克)中,其频率分布直方图如图所示.
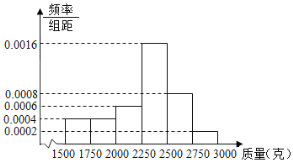
(1)按分层抽样的方法从质量落在![]() ,
,![]() 的蜜柚中抽取5个,再从这5个蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
的蜜柚中抽取5个,再从这5个蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
(2)以各组数据的中间数代表这组数据的平均水平,以频率代表概率,已知该贫困村的蜜柚树上大约还有5000个蜜柚等待出售,某电商提出两种收购方案:
A. 所有蜜柚均以40元/千克收购;
B. 低于2250克的蜜柚以60元/个收购,高于或等于2250克的以80元/个收购.
请你通过计算为该村选择收益最好的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com