
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| P | n-1 |
| 1 |
| 2 |
| P | n-2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省绵阳市南山中学高二(下)期中数学试卷(理科)(解析版) 题型:解答题
 .棋盘上标有第0站、第1站、第2站、…、第m(m∈N,m≥100)站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第m-1站(胜利大本营)或第m站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn.
.棋盘上标有第0站、第1站、第2站、…、第m(m∈N,m≥100)站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第m-1站(胜利大本营)或第m站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn. .
.查看答案和解析>>
科目:高中数学 来源:2010年江西省南昌十六中高考数学一模试卷(文科)(解析版) 题型:解答题
 .棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn.
.棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn. ;(n≤99,n∈N)
;(n≤99,n∈N)查看答案和解析>>
科目:高中数学 来源:2007年江苏省苏州市木渎高级中学高考数学模拟试卷(解析版) 题型:解答题
 .棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn.
.棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋子向前跳一站;若掷出反面,则棋子向前跳两站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为Pn.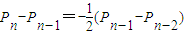 ;(n≤99,n∈N)
;(n≤99,n∈N)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com