
【题目】已知函数![]() .
.
(Ⅰ)求证:对于任意![]() ,不等式
,不等式![]() 恒成立;
恒成立;
(Ⅱ)设函数![]() ,
,![]() ,求函数
,求函数![]() 的最小值.
的最小值.
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C的极坐标方程为![]() .以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
.以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为![]() (t为参数)
(t为参数)
(1)若![]() ,求曲线C的直角坐标方程以及直线l的极坐标方程;
,求曲线C的直角坐标方程以及直线l的极坐标方程;
(2)设点![]() ,曲线C与直线
,曲线C与直线![]() 交于A、B两点,求
交于A、B两点,求![]() 的最小值
的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设首项为a1的正项数列{an}的前n项和为Sn,q为非零常数,已知对任意正整数n,m,Sn+m=Sm+qmSn总成立.
(1)求证:数列{an}是等比数列;
(2)若不等的正整数m,k,h成等差数列,试比较ammahh与ak2k的大小;
(3)若不等的正整数m,k,h成等比数列,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
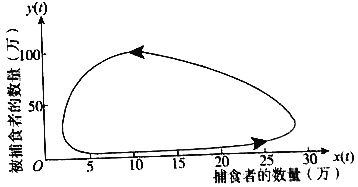
【题目】假设存在两个物种,前者有充足的食物和生存空间,而后者仅以前者为食物,则我们称前者为被捕食者,后者为捕食者.现在我们来研究捕食者与被捕食者之间理想状态下的数学模型.假设捕食者的数量以![]() 表示,被捕食者的数量以
表示,被捕食者的数量以![]() 表示.如图描述的是这两个物种随时间变化的数量关系,其中箭头方向为时间增加的方向.下列说法正确的是( )
表示.如图描述的是这两个物种随时间变化的数量关系,其中箭头方向为时间增加的方向.下列说法正确的是( )
A.若在![]() 、
、![]() 时刻满足:
时刻满足:![]() ,则
,则![]()
B.如果![]() 数量是先上升后下降的,那么
数量是先上升后下降的,那么![]() 的数量一定也是先上升后下降
的数量一定也是先上升后下降
C.被捕食者数量与捕食者数量不会同时到达最大值或最小值
D.被捕食者数量与捕食者数量总和达到最大值时,被捕食者的数量也会达到最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,函数g(x)=kx﹣cosx在点![]() 处的切线平行于x轴.
处的切线平行于x轴.
(1)求函数f(x)的极值;
(2)讨论函数F(x)=g(x)﹣f(x)的零点的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com