
 =
=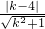 ,化简得:-k=k-4或k=k-4(无解),解得k=2,
,化简得:-k=k-4或k=k-4(无解),解得k=2,

 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
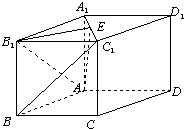 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为a的菱形,且∠ABC=60°,侧棱长为
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为a的菱形,且∠ABC=60°,侧棱长为
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市高三模拟考试理科数学 题型:解答题
(本题满分18分,其中第1小题4分,第2小题6分,第,3小题8分)
一青蛙从点 开始依次水平向右和竖直向上跳动,其落点坐标依次是
开始依次水平向右和竖直向上跳动,其落点坐标依次是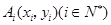 ,(如图所示,
,(如图所示, 坐标以已知条件为准),
坐标以已知条件为准), 表示青蛙从点
表示青蛙从点 到点
到点 所经过的路程。
所经过的路程。
(1) 若点 为抛物线
为抛物线
 准线上
准线上
一点,点 ,
, 均在该抛物线上,并且直线
均在该抛物线上,并且直线
 经
经
过该抛物线的焦点,证明 .
.
(2)若点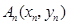 要么落在
要么落在 所表示的曲线上,
所表示的曲线上,
要么落在 所表示的曲线上,并且
所表示的曲线上,并且 ,
,
试写出 (不需证明);
(不需证明);
(3)若点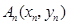 要么落在
要么落在 所表示的曲线上,要么落在
所表示的曲线上,要么落在 所表示的曲线上,并且
所表示的曲线上,并且 ,求
,求 的表达式.
的表达式.

查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省台州市玉环县玉城中学高二(上)第二次月考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省常州中学高三最后冲刺综合练习数学试卷4(文科)(解析版) 题型:解答题
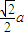 ,若经过AB1且与BC1平行的平面交上底面线段A1C1于点E.
,若经过AB1且与BC1平行的平面交上底面线段A1C1于点E.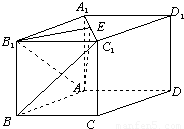
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com