(本小题满分14分)
已知函数
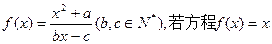
有且只有两个相异实根0,2,且
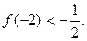
(Ⅰ)求函数
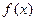
的解析式;
(Ⅱ)已知各项均不为1的数列
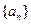
满足
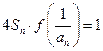
,求通
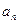
,
(Ⅲ)设
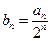
,求数列
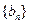
的前
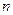
项和
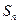
.
解:(Ⅰ)由
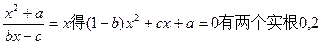
得

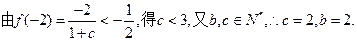
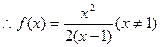
(Ⅱ)

即为

①
当

②
①-②则
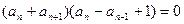
,
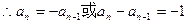
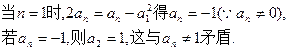
所以
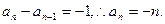
(Ⅲ)由(Ⅱ)知
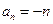
,所以
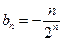
故
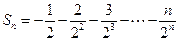
③
上式两边乘以
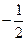
得
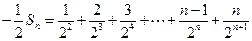
④
③+④得

∴
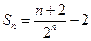
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(10分)已知函数
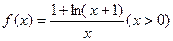
(1)判断函数
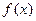
在区间
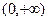
上的单调性;(2)若当
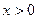
时,
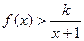
恒成立,求正整数
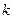
的最大值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
已知
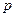
:函数
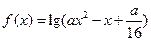
的定义域为
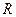
;
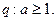
如果命题“
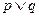
为真,
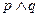
为假”,求实数
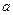
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分9分)
已知函数
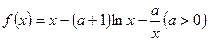
。
(Ⅰ)当
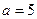
时,求函数
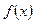
的单调递增区间;
(Ⅱ)求
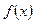
的极大值;
(Ⅲ)求证:对于任意
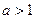
,函数
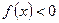
在
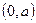
上恒成立。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题9分)设函数
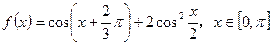
。
(1)求
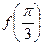
的值;
(2)求

的最小值及

取最小值时
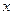
的集合;(3)求

的单调递增区间。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数
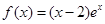
的单调递增区间是
A. | B.(0,2) | C.(1,3) | D.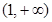 |
查看答案和解析>>

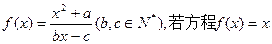 有且只有两个相异实根0,2,且
有且只有两个相异实根0,2,且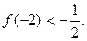
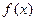 的解析式;
的解析式; 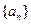 满足
满足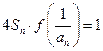 ,求通
,求通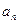 ,
,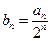 ,求数列
,求数列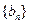 的前
的前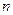 项和
项和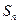 .
.