
【题目】在![]() 中,内角
中,内角![]() 、
、![]() 、
、![]() 所对的边分别是
所对的边分别是![]() 、
、![]() 、
、![]() ,不等式
,不等式![]() 对一切实数
对一切实数![]() 恒成立.
恒成立.
(1)求![]() 的取值范围;
的取值范围;
(2)当![]() 取最大值,且
取最大值,且![]() 的周长为
的周长为![]() 时,求
时,求![]() 面积的最大值,并指出面积取最大值时
面积的最大值,并指出面积取最大值时![]() 的形状.(参考知识:已知
的形状.(参考知识:已知![]() 、
、![]() ,
,![]() ;
;![]() 、
、![]() ,
,![]() )
)
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了50名市民,得到数据如下表:
喜欢 | 不喜欢 | 合计 | |
大于40岁 | 20 | 5 | 25 |
20岁至40岁 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(1)判断是否有99.5%的把握认为喜欢“人文景观”景点与年龄有关?(![]() 保留小数点后3位)
保留小数点后3位)
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取3人作进一步调查,将这3位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位鼓励员工参加健身运动,推广了一款手机软件,记录每人每天走路消耗的卡路里;软件的测评人员从员工中随机地选取了40人(男女各20人),记录他们某一天消耗的卡路里,并将数据整理如下:

(1)已知某人一天的走路消耗卡路里超过180千卡被评测为“积极型”,否则为“懈怠型”,根据题中数据完成下面的![]() 列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?

(2)若测评人员以这40位员工每日走路所消耗的卡路里的频率分布来估计其所有员工每日走路消耗卡路里的频率分布,现在测评人员从所有员工中任选2人,其中每日走路消耗卡路里不超过120千卡的有![]() 人,超过210千卡的有
人,超过210千卡的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:  ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过市场调查,某种商品在销售中有如下关系:第x(1≤x≤30,x∈N+)天的销售价格(单位:元/件)为f(x)=![]() 第x天的销售量(单位:件)为g(x)=a-x(a为常数),且在第20天该商品的销售收入为1 200元(销售收入=销售价格×销售量).
第x天的销售量(单位:件)为g(x)=a-x(a为常数),且在第20天该商品的销售收入为1 200元(销售收入=销售价格×销售量).
(1)求a的值,并求第15天该商品的销售收入;
(2)求在这30天中,该商品日销售收入y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点.
两点.
(1)若以![]() 为直径的动圆内切于圆
为直径的动圆内切于圆![]() ,求椭圆的长轴长;
,求椭圆的长轴长;
(2)当![]() 时,问在
时,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?并说明理由.
为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·牡丹江一中]某校从参加高一年级期末考试的学生中抽取60名学生的成绩(均为整数),其成绩的频率分布直方图如图所示,由此估计此次考试成绩的中位数,众数和平均数分别是( )
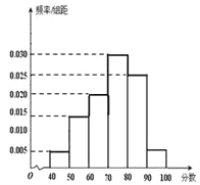
A. 73.3,75,72 B. 73.3,80,73
C. 70,70,76 D. 70,75,75
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com