�⣺����f
1��x��=x
2��C������֤�����£�
������ʵ��x
1��x
2�����ʣ�0��1����
��f����x
1+��1-����x
2��-��f��x
1��-��1-����f��x
2��=����x
1+��1-����x
2��
2-��x
12-��1-����x
22=-����1-����x
12-����1-����x
22+2����1-����x
1x
2=-����1-������x
1-x
2��
2��0��
��f����x
1+��1-����x
2���ܦ�f��x
1��+��1-����f��x
2����
��f
1��x��=x
2��C������
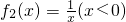
����C������֤�����£�
ȡx
1=-3��x
2=-1��
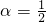
��
��f����x
1+��1-����x
2��-��f��x
1��-��1-����f��x
2��=

��
��f����x
1+��1-����x
2������f��x
1��+��1-����f��x
2����
��
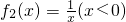
����C������
��������0��n��m��ȡx
1=m��x
2=0��
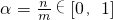
��
��f��x����R�ϵ���������a
n=f��n������a
0=0��a
m=2m
��a
n=f��n��=f����x
1+��1-����x
2���ܦ�f��x
1��+��1-����f��x
2��=
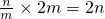
��
��ôS
f=a
1+a
2+��+a
m��2����1+2+��+m��=m
2+m��
��֤f��x��=2x��C��������ʹ��a
n=2n��n=0��1��2������m������������ʱS
f=m
2+m��
����������S
f�����ֵΪm
2+m��
������g��x����R�ϵ�C������
������m��n��m��n��[0��T]ʹ��g��m����g��n����
��g��m����g��n������

����0������1����n=��x
1+��1-����x
2��ôg��n��=g[��x
1+��1-����x
2]�ܦ�g��x
1��+��1-����g��x
2��=g��m��
����g��m����g��n��ì�ܣ�
��g��m����g��n����
��
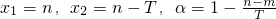
Ҳ�ɵõ�ì�ܣ�
��g��x����[0��T]���dz�������������Ϊg��x��������ΪT�ĺ���������g��x����R���dz�������������g��x������С������ΪTì�ܣ�
����g��x������R�ϵ�C������ ��14�֣�
����������f
1��x��=x
2��C������ֱ����f����x
1+��1-����x
2��-��f��x
1��-��1-����f��x
2�����Ƴ���С�ڵ���0���ɣ�
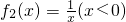
����C���������þٷ����ķ������ɣ�x
1=-3��x
2=-1��
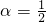
��
�����ȸ��ݶ������a
n=f��n���ķ�Χ���ٽ�϶��弴�����S
f�����ֵ���ɣ�
������g��x����R�ϵ�C������������m��n��m��n��[0��T]ʹ��g��m����g��n������g��m����g��n����g��m����g��n�������÷�֤��������֤��g��x������R�ϵ�C������
������������Ҫ�����¶����¿����������⣮���������һ�������������һ��f��x����a�������ֻ���f��x������СֵС���ɣ�����f��x����a�������ֻ���f��x�������ֵ�ɣ�

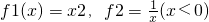 �Ƿ�Ϊ���Զ������ϵ�C��������˵�����ɣ�
�Ƿ�Ϊ���Զ������ϵ�C��������˵�����ɣ�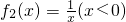 ����C������֤�����£�
����C������֤�����£�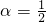 ��
�� ��
��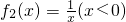 ����C������
����C������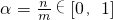 ��
��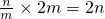 ��
�� ����0������1����n=��x1+��1-����x2
����0������1����n=��x1+��1-����x2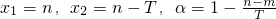 Ҳ�ɵõ�ì�ܣ�
Ҳ�ɵõ�ì�ܣ�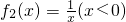 ����C���������þٷ����ķ������ɣ�x1=-3��x2=-1��
����C���������þٷ����ķ������ɣ�x1=-3��x2=-1��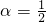 ��
��


 ��
�� ��
�� ����
����



