
【题目】已知函数![]() ,
,![]() .
.
(I)设![]() ,求
,求![]() 的单调区间;
的单调区间;
(II)若![]() 在
在![]() 处取得极大值,求实数
处取得极大值,求实数![]() 的取值范围.
的取值范围.
【答案】(I)单调增区间是![]() ,单调减区间是
,单调减区间是![]() .(II)
.(II)![]()
【解析】
试题分析:(I)![]() ,先求
,先求![]() 导函数
导函数![]() ,求导函数零点
,求导函数零点![]() ,列表分析导函数符号变化规律,确定单调区间(II)由题意得
,列表分析导函数符号变化规律,确定单调区间(II)由题意得![]() ,且
,且![]() 最大值;
最大值;![]() 最大值;而
最大值;而![]() 所以
所以![]() ,也可分类讨论单调性变化规律
,也可分类讨论单调性变化规律
试题解析:解:(I)∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() .
.
当![]() 时,在
时,在![]() 上
上![]() ,
,![]() 单调递增;
单调递增;
在![]() 上
上![]() ,
,![]() 单调递减.
单调递减.
∴![]() 的单调增区间是
的单调增区间是![]() ,单调减区间是
,单调减区间是![]() .
.
(II)∵![]() 在
在![]() 处取得极大值,∴
处取得极大值,∴![]() .
.
①当![]() ,即
,即![]() 时,由(I)知
时,由(I)知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() ,
,![]() 单调递减,不合题意;
单调递减,不合题意;
②当![]() ,即
,即![]() 时,由(I)知,
时,由(I)知,![]() 在
在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 处取得极小值,不合题意;
处取得极小值,不合题意;
③当![]() ,即
,即![]() 时,由(I)知,
时,由(I)知,![]() 在
在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() 取得极大值,满足条件.
取得极大值,满足条件.
综上,实数![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
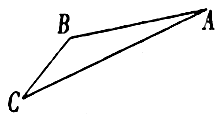
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD是块矩形硬纸板,其中AB=2AD,AD=![]() ,E为DC的中点,将它沿AE折成直二面角D-AE-B.
,E为DC的中点,将它沿AE折成直二面角D-AE-B.

(1)求证:AD⊥平面BDE;
(2)求二面角B-AD-E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,两条公路AP与AQ夹角A为钝角,其正弦值是![]()
![]() .甲乙两人从A点出发沿着两条公路进行搜救工作,甲沿着公路AP方向,乙沿着公路AQ方向.
.甲乙两人从A点出发沿着两条公路进行搜救工作,甲沿着公路AP方向,乙沿着公路AQ方向.

(1)当甲前进5km的时候到达P处,同时乙到达Q处,通讯测得甲乙两人相距![]()
![]() km,求乙在此时前进的距离AQ;
km,求乙在此时前进的距离AQ;
(2)甲在5公里处原地未动,乙回头往A方向行走至M点收到甲发出的信号,此时M点看P、Q两点的张角为![]() (张角为
(张角为![]() QMP)
QMP)![]() ,求甲乙两人相距的距离MP的长.
,求甲乙两人相距的距离MP的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对高一年级学生寒假参加社区服务的次数进行了统计,随机抽取了![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:

(1)求表中![]() 的值和频率分布直方图中
的值和频率分布直方图中![]() 的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
(2)如果用分层抽样的方法从样本服务次数在![]() 和
和![]() 的人中共抽取6人,再从这6人中选2人,求2人服务次数都在
的人中共抽取6人,再从这6人中选2人,求2人服务次数都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(4, 0),B(2, 2),C (6, 0),记△ABC的外接圆为⊙P.
(1)求⊙P的方程.
(2)对于线段PA上的任意一点G,是否存在以B为圆心的圆,在圆B上总能找到不同的两点E、F,满足![]() =
=![]() ,若存在,求圆B的半径
,若存在,求圆B的半径![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂有容量300吨的水塔一个,每天从早六点到晚十点供应生活和生产用水,已知:该厂生活用水每小时10吨,工业用水总量![]() (吨)与时间
(吨)与时间![]() (单位:小时,规定早晨六点时
(单位:小时,规定早晨六点时![]() )的函数关系为
)的函数关系为![]() ,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级, 进水量增加10吨.若某天水塔原有水100吨,在供应同时打开进水管.问该天进水量应选择几级,既能保证该厂用水(即水塔中水不空),又不会使水溢出?
,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级, 进水量增加10吨.若某天水塔原有水100吨,在供应同时打开进水管.问该天进水量应选择几级,既能保证该厂用水(即水塔中水不空),又不会使水溢出?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com