
【题目】为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人 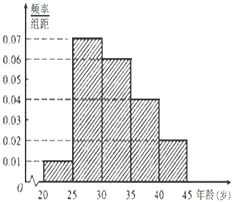
(1)求该组织的人数;
(2)若从该组织年龄在[20,25),[25,30),[30,35)内的成员中用分层抽样的方法共抽取14名志愿者参加某社区的宣传活动,问应各抽取多少名志愿者?
【答案】
(1)解:由频率分布直方图知年龄在[35,40)内频率为5×0.04=0.20,
又∵年龄在[35,40)内有20人,
∴该组织的人数n= ![]() 人.
人.
(2)解:年龄在[20,25),[25,30).[30,35)内的人数分别为:
0.01×5×100=5,0.07×5×100=35,0.06×5×100=30,
利用分层抽样方法从中抽取14名志愿者,
年龄在[20,25)内应抽取的人数为: ![]() =1人,
=1人,
年龄在[25,30)内应抽取人数为 ![]() 人,
人,
年龄在[30,35)内应抽取人数为 ![]() ,
,
∴应从年齡在[20,25),[25,30)[30,35)内分别抽取 1人,2人,6人
【解析】(1)由频率分布直方图求出年龄在[35,40)内频率,作年龄在[35,40)内有人数,由此能求出该组织的人数.(2)年龄在[20,25),[25,30).[30,35)内的人数,由此利用分层抽样方法从中抽取14名志愿者,能求出应从年齡在[20,25),[25,30)[30,35)内分别抽取多少人.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为3 ![]() ,b﹣c=2,cosA=﹣
,b﹣c=2,cosA=﹣ ![]() .
.
(1)求a和sinC的值;
(2)求cos(2A+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x-3)ex+ax,aR
(1)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程;
(2)当a[0,e)时,设函数f(x)在(1,+)上的最小值为g(a),求函数g(a)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() cos2x+sin2(x+
cos2x+sin2(x+ ![]() ). (Ⅰ)求f(x)的最小正周期和单调递增区间;
). (Ⅰ)求f(x)的最小正周期和单调递增区间;
(Ⅱ)当x∈[﹣ ![]() ,
, ![]() )时,求f(x)的取值范围.
)时,求f(x)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(sin
=(sin ![]() x,cos
x,cos ![]() x),
x), ![]() =(sin
=(sin ![]() x,
x, ![]() sin
sin ![]() x),x∈R,函数f(x)=
x),x∈R,函数f(x)= ![]() ,求:
,求:
(1)f(x)的最小正周期;
(2)f(x)在区间[0,1]上的最大值和最小值,以及取得最大值和最小值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点. 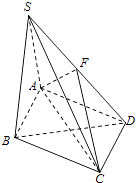
(1)求三棱锥S﹣FAC的体积;
(2)求直线BD与平面FAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学校本课程开设了A,B,C,D共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生.
(1)求这3名学生选修课所有选法的总数;
(2)求恰有2门选修课没有被这3名学生选择的概率;
(3)求A选修课被这3名学生选择的人数ξ的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com