
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,
,![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 且与
且与![]() 轴不重合的直线
轴不重合的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过点
为直径的圆过点![]() .
.
(ⅰ)求![]() 的方程;
的方程;
(ⅱ)记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加.下表是某购物网站2017年1-8月促销费用(万元)和产品销量(万件)的具体数据.

(1)根据数据可知![]() 与
与![]() 具有线性相关关系,请建立
具有线性相关关系,请建立![]() 关于
关于![]() 的回归方程
的回归方程![]() (系数精确到
(系数精确到![]() );
);
(2)已知6月份该购物网站为庆祝成立1周年,特制定奖励制度:以![]() (单位:件)表示日销量,
(单位:件)表示日销量, ![]() ,则每位员工每日奖励100元;
,则每位员工每日奖励100元; ![]() ,则每位员工每日奖励150元;
,则每位员工每日奖励150元; ![]() ,则每位员工每日奖励200元.现已知该网站6月份日销量
,则每位员工每日奖励200元.现已知该网站6月份日销量![]() 服从正态分布
服从正态分布![]() ,请你计算某位员工当月奖励金额总数大约多少元.(当月奖励金额总数精确到百分位)
,请你计算某位员工当月奖励金额总数大约多少元.(当月奖励金额总数精确到百分位)
参考数据: ![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量, ![]() .
.
参考公式:
(1)对于一组数据![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为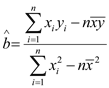 ,
, ![]() .
.
(2)若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an} 和等比数列{bn}满足a1=b1=1,a2+a4=10,b2b4=a5.
(1)求{an}的通项公式;
(2)求和:b1+b3+b5+…+b2n-1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一、高二年级的全体学生都参加了体质健康测试,测试成绩满分为100分,规定测试成绩在![]() 之间为“体质优秀”,在
之间为“体质优秀”,在![]() 之间为“体质良好”,在
之间为“体质良好”,在![]() 之间为“体质合格”,在
之间为“体质合格”,在![]() 之间为“体质不合格”
之间为“体质不合格”![]() 现从两个年级中各随机抽取8名学生,测试成绩如下:
现从两个年级中各随机抽取8名学生,测试成绩如下:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
高一年级 | 60 | 85 | 55 | 80 | 65 | 90 | 90 | 75 |
高二年级 | 75 | 85 | 65 | 90 | 75 | 60 | a | b |
其中a,b是正整数.
(1)若该校高一年级有200名学生,试估计高一年级“体质优秀”的学生人数;
(2)从高一年级抽取的学生中再随机选取3人,求这3人中,恰有1人“体质良好”的概率;
(3)设两个年级被抽取学生的测试成绩的平均数相等,当高二年被抽取学生的测试成绩的方差最小时,写出a,b的值![]() 结论不要求证明
结论不要求证明![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求定义域,并判断函数f(x)的奇偶性;
(2)若f(1)+f(2)=0,证明函数f(x)在(0,+∞)上的单调性,并求函数f(x)在区间[1,4]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中文“函数”(function)一词,最早由近代数学家李善兰翻译的之所以这么翻译,他给出的原因是“凡此变数中函彼变数者,则此为彼之函数”,也即函数指一个量随着另一个量的变化而变化下列选项中两个函数相等的是( )
A.![]() 与
与![]() B.
B.![]() 与
与![]()
C.![]() 与
与![]() D.
D.![]() 与
与![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com