
【题目】设函数f(x)=Asin(ωx+φ)(A>0,ω>0,﹣ ![]() <φ<
<φ< ![]() ,x∈R)的部分图象如图所示.
,x∈R)的部分图象如图所示. 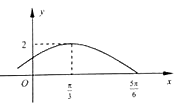
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)将函数y=f(x)的图象沿x轴方向向右平移 ![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的 ![]() (纵坐标不变),得到函数y=g(x)的图象,当x∈[﹣
(纵坐标不变),得到函数y=g(x)的图象,当x∈[﹣ ![]() ,
, ![]() ]时,求函数g(x)的值域.
]时,求函数g(x)的值域.
【答案】解:(Ⅰ)由图象知,A=2,
又 ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() ,ω>0,
,ω>0,
所以T=2π= ![]() ,得ω=1.
,得ω=1.
所以f(x)=2sin(x+φ),
将点( ![]() ,2)代入,得
,2)代入,得 ![]() +φ=2kπ+
+φ=2kπ+ ![]() (k∈Z),
(k∈Z),
即φ= ![]() +2kπ(k∈Z),又﹣
+2kπ(k∈Z),又﹣ ![]() <φ<
<φ< ![]() ,
,
所以,φ= ![]() .
.
所以f(x)=2sin(x+ ![]() ).
).
故函数y=f(x)的解析式为:f(x)=2sin(x+ ![]() ).
).
(Ⅱ)将函数y=f(x)的图象沿x轴方向右平移 ![]() 个单位长度,
个单位长度,
得到的图象对应的解析式为:y=2sinx,
再把横坐标缩短到原来的 ![]() (纵坐标不变),得到的图象对应的解析式为:g(x)=2sin2x,
(纵坐标不变),得到的图象对应的解析式为:g(x)=2sin2x,
∵x∈[﹣ ![]() ,
, ![]() ],
],
∴﹣ ![]() ≤2x≤
≤2x≤ ![]() ,
,
∴2sin2x∈[﹣1,2],可得:g(x)∈[﹣1,2]
【解析】(Ⅰ)由图象知,A,周期T,利用周期公式可求ω,由点( ![]() ,2)在函数图象上,结合范围﹣
,2)在函数图象上,结合范围﹣ ![]() <φ<
<φ< ![]() ,可求φ,从而解得函数解析式.(Ⅱ)由函数y=Asin(ωx+φ)的图象变换规律可求g(x),利用正弦函数的图象和性质即可得解.
,可求φ,从而解得函数解析式.(Ⅱ)由函数y=Asin(ωx+φ)的图象变换规律可求g(x),利用正弦函数的图象和性质即可得解.
【考点精析】解答此题的关键在于理解函数y=Asin(ωx+φ)的图象变换的相关知识,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是( )
A.(﹣∞,﹣3)∪(0,3)
B.(﹣∞,﹣3)∪(3,+∞)
C.(﹣3,0)∪(3,+∞)
D.(﹣3,0)∪(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,底面ABC等边三角形,E,F分别是BC,CC1的中点.求证: (Ⅰ) EF∥平面A1BC1;
(Ⅱ) 平面AEF⊥平面BCC1B1 . 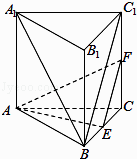
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣3=0.
(1)求圆的圆心C的坐标和半径长;
(2)直线l经过坐标原点且不与y轴重合,l与圆C相交于A(x1 , y1)、B(x2 , y2)两点,求证: ![]() 为定值;
为定值;
(3)斜率为1的直线m与圆C相交于D、E两点,求直线m的方程,使△CDE的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2ax+4(0<a<3),若x1<x2 , x1+x2=1﹣a,则( )
A.f(x1)<f(x2)
B.f(x1)>f(x2)
C.f(x1)=f(x2)
D.f(x1)<f(x2)和f(x1)=f(x2)都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣2a|+a2﹣4a(a∈R). (Ⅰ)当a=﹣1时,求f(x)在[﹣3,0]上的最大值和最小值;
(Ⅱ)若方程f(x)=0有3个不相等的实根x1 , x2 , x3 , 求 ![]() +
+ ![]() +
+ ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=cos(2x﹣ ![]() )的图象,只需将函数y=sin2x的图象( )
)的图象,只需将函数y=sin2x的图象( )
A.向左平移 ![]() 个单位
个单位
B.向左平移 ![]() 个单位
个单位
C.向右平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究.全年级共有1350人,男女生比例为8:7,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为 ![]() ,通过对被抽取学生的问卷调查,得到如下2x2列联表:
,通过对被抽取学生的问卷调查,得到如下2x2列联表:
支持 | 反对 | 总计 | |
男生 | 30 | ||
女生 | 25 | ||
总计 |
(Ⅰ)完成列联表,并判断能否有99.9%的把握认为态度与性别有关?
(Ⅱ)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界表:K2= ![]()
P(K2≥k0) | 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
k0 | 2.706% | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,侧面ABC是一个等腰直角三角形,∠BAC=90°,底面BCD是一个等边三角形,平面ABC⊥平面BCD,E为BD的中点,则AE与平面BCD所成角的大小为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com