
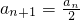 ;当an为奇数时,
;当an为奇数时,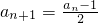 .
.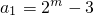 (m≥3且m∈N),数列{an}的前n项和为Sn,求证:
(m≥3且m∈N),数列{an}的前n项和为Sn,求证: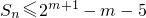 .
.解:(1)由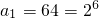 ,可得
,可得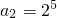 ,
,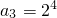 ,…,
,…,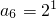 ,
,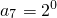 ,
,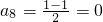 ,a9=0,…,
,a9=0,…,
即{an}的前7项成等比数列,从第8起数列的项均为0.
故数列{an}的通项公式为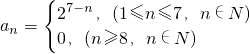 .
.
(2)若a1=4k(k∈Z)时,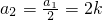 ,
,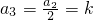 ,
,
由a1,a2,a3成等差数列,可知即2(2k)=k+4k,解得k=0,故a1=0;
若a1=4k+1(k∈Z)时,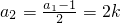 ,
,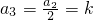
由a1,a2,a3成等差数列,可知2(2k)=(4k+1)+k,解得k=-1,故a1=-3;
若a1=4k+2(k∈Z)时,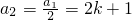 ,
,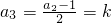 ,
,
由a1,a2,a3成等差数列,可知2(2k+1)=(4k+2)+k,解得k=0,故a1=2;
若a1=4k+3(k∈Z)时,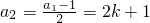 ,
,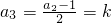 ,
,
由a1,a2,a3成等差数列,可知2(2k+1)=(4k+3)+k,解得k=-1,故a1=-1;
∴a1的值为-3,-1,0,2.
(3)由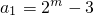 (m≥3),可得
(m≥3),可得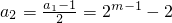 ,
,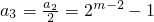 ,
,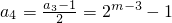 ,
,
若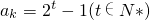 ,则ak是奇数,从而
,则ak是奇数,从而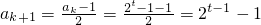 ,
,
可得当3≤n≤m+1时,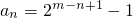 成立.
成立.
又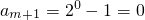 ,am+2=0,…
,am+2=0,…
故当n≤m时,an>0;当n≥m+1时,an=0.
故对于给定的m,Sn的最大值为a1+a2+…+am=(2m-3)+(2m-1-2)+(2m-2-1)+(2m-3-1)+…+(21-1)=(2m+2m-1+2m-2+…+21)-m-3=2m+1-m-5,
故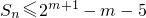 .
.
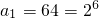 ,可得{an}的前7项成等比数列,从第8起数列的项均为0,从而利用分段函数的形式写出数列{an}的通项公式即可;
,可得{an}的前7项成等比数列,从第8起数列的项均为0,从而利用分段函数的形式写出数列{an}的通项公式即可;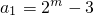 (m≥3),可得a2,a3,a4.若
(m≥3),可得a2,a3,a4.若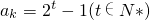 ,则ak是奇数,可得当3≤n≤m+1时,
,则ak是奇数,可得当3≤n≤m+1时,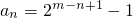 成立,又当n≤m时,an>0;当n≥m+1时,an=0.故对于给定的m,Sn的最大值为2m+1-m-5,即可证出结论.
成立,又当n≤m时,an>0;当n≥m+1时,an=0.故对于给定的m,Sn的最大值为2m+1-m-5,即可证出结论.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:高中数学 来源: 题型:
| an |
| 2 |
| an-1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an |
| 2 |
| an-1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2013年上海市黄浦区高考数学二模试卷(理科)(解析版) 题型:解答题
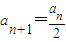 ;当an为奇数时,
;当an为奇数时,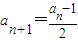 .
.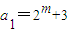 (m>3且m∈N),数列{an}的前n项和为Sn,求证:
(m>3且m∈N),数列{an}的前n项和为Sn,求证: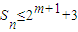 ;
;查看答案和解析>>
科目:高中数学 来源:2013年上海市黄浦区高考数学二模试卷(文科)(解析版) 题型:解答题
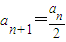 ;当an为奇数时,
;当an为奇数时,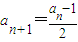 .
.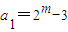 (m≥3且m∈N),数列{an}的前n项和为Sn,求证:
(m≥3且m∈N),数列{an}的前n项和为Sn,求证: .( )
.( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com