
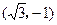 ,b=
,b=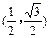
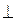 b;
b;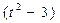 b,y=-ka+tb,且x
b,y=-ka+tb,且x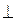 y,试求k,t的函数关系式
y,试求k,t的函数关系式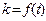 ;
;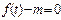 的解的情况。
的解的情况。
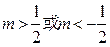 时,直线k=m与曲线
时,直线k=m与曲线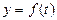 仅有一个交点,则方程有一解;
仅有一个交点,则方程有一解;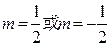 时,直线k=m与曲线
时,直线k=m与曲线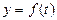 有两个交点,则方程有两解;
有两个交点,则方程有两解;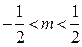 时,直线k=m与曲线
时,直线k=m与曲线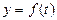 有三个交点,则方程有三个解。
有三个交点,则方程有三个解。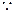 a·b
a·b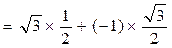 =0,
=0,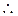 a
a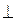 b。
b。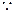 x
x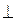 y,
y,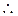 x·y=0,即〔a+
x·y=0,即〔a+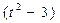 b〕·(—ka+tb)=0
b〕·(—ka+tb)=0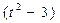 〕a·b+t
〕a·b+t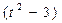 b2=0
b2=0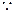 a·b=0,a2=4,b2=1。
a·b=0,a2=4,b2=1。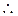 上式化为-4k+ t
上式化为-4k+ t 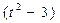 =0,
=0,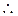 k=
k=
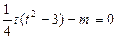 的解得情况,可以看做曲线
的解得情况,可以看做曲线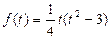 与直线k=m的交点个数。
与直线k=m的交点个数。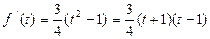 。
。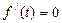 ,解得
,解得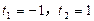 ,当
,当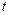 变化时,
变化时,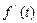 、
、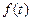 的变化情况如下表:
的变化情况如下表: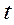 | 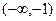 | 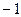 | 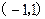 | 1 | 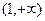 |
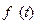 | 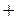 | 0 | - | 0 | + |
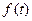 | 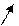 | 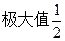 |  | 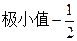 |  |
 时,
时,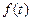 有极大值,极大值为
有极大值,极大值为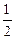 。
。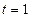 时,
时,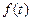 有极小值,极小值为
有极小值,极小值为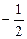 。
。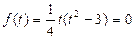 时,得
时,得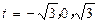 。 所以
。 所以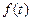 的图像大致如图所示
的图像大致如图所示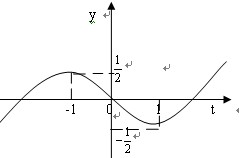
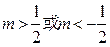 时,直线k=m与曲线
时,直线k=m与曲线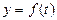 仅有一个交点,则方程有一解;
仅有一个交点,则方程有一解;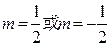 时,直线k=m与曲线
时,直线k=m与曲线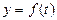 有两个交点,则方程有两解;
有两个交点,则方程有两解;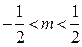 时,直线k=m与曲线
时,直线k=m与曲线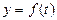 有三个交点,则方程有三个解。
有三个交点,则方程有三个解。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com