
【题目】本公司计划2018年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为![]() 元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
【答案】该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告,公司的收益最大,最大收益是70万元.
【解析】试题分析: 先根据题意列约束条件以及目标函数,再作可行域,根据目标函数线平移确定最大值取法,最后利用解方程组得最优解.
试题解析:设公司在甲电视台和乙电视台做广告的时间分别为![]() 分钟和
分钟和![]() 分钟,总收益为
分钟,总收益为![]() 元,由题意得
元,由题意得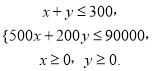
目标函数为![]() .
.
二元一次不等式组等价于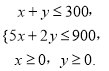
作出二元一次不等式组所表示的平面区域,
即可行域. 如图:
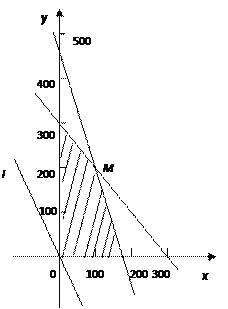
作直线![]() ,
,
即![]() .
.
平移直线![]() ,从图中可知,当直线
,从图中可知,当直线![]() 过
过![]() 点时,
点时,
目标函数取得最大值.
联立![]() 解得
解得![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() (元).
(元).
答:该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告,公司的收益最大,最大收益是70万元.


科目:高中数学 来源: 题型:
【题目】某研究机构对中学生记忆能力x和识图能力y进行统计分析,得到如下数据:
记忆能力x | 4 | 6 | 8 | 10 |
识图能力y | 3 | ﹡﹡﹡ | 6 | 8 |
由于某些原因,识图能力的一个数据丢失,但已知识图能力样本平均值是5.5.
(Ⅰ)求丢失的数据;
(Ⅱ)经过分析,知道记忆能力x和识图能力y之间具有线性相关关系,请用最小二乘法求出y关于x的线性回归方程 ![]() ;
;
(III)若某一学生记忆能力值为12,请你预测他的识图能力值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出了2010年亚洲一些国家的国民平均寿命(单位:岁)
国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 |
阿曼 76.1 | 泰国 73.7 | 阿富汗 59.0 | 尼泊尔 68.0 | 孟加拉国 70.1 |
(1)请补齐频率分布表,并求出相应频率分布直方图中的a,b;
分组 | 频数 | 频率 |
[59.0,63.0) | 2 | 0.05 |
[63.0,67.0) | ||
[67.0,71.0) | ||
[71.0,75.0) | 9 | 0.225 |
[75.0,7.0) | 7 | 0.175 |
[79.0,83.0] | 5 | 0.125 |
合计 | 40 | 1.00 |
(2)请根据统计思想,利用(1)中的频率分布直方图估计亚洲人民的平均寿命. 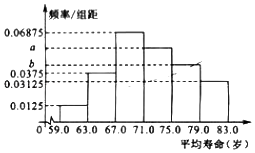
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com