
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的离心率是
的离心率是![]() ,斜率不为0的直线
,斜率不为0的直线![]() :
:![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() .
.
(1)若![]() 、
、![]() 分别是
分别是![]() 的左、右焦点,当
的左、右焦点,当![]() 经过
经过![]() 且
且![]() 时,求
时,求![]() 的值;
的值;
(2)试探究,是否存在点![]() ,使得
,使得![]() ?若存在,请写出满足条件的
?若存在,请写出满足条件的![]() 、
、![]() 的关系式;若不存在,说明理由.
的关系式;若不存在,说明理由.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:
【题目】某中学2018年的高考考生人数是2015年高考考生人数的![]() 倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:
倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:

则下列结论正确的是![]()
![]()
A. 与2015年相比,2018年一本达线人数减少
B. 与2015年相比,2018年二本达线人数增加了![]() 倍
倍
C. 2015年与2018年艺体达线人数相同
D. 与2015年相比,2018年不上线的人数有所增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2011年国际数学协会正式宣布,将每年的3月14日设为国际数学节,来源于中国古代数学家祖冲之的圆周率。公元263年,中国数学家刘徽用“割圆术”计算圆周率,计算到圆内接3072边形的面积,得到的圆周率是![]() .公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率
.公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率![]() 和约率
和约率![]() 。大约在公元530年,印度数学大师阿耶波多算出圆周率约为
。大约在公元530年,印度数学大师阿耶波多算出圆周率约为![]() (
(![]() ).在这4个圆周率的近似值中,最接近真实值的是( )
).在这4个圆周率的近似值中,最接近真实值的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学成就甚大,在世界科技史上占有重要的地位.“算经十书”是汉、唐千余年间陆续出现的10部数学著作,包括《周髀算经》、《九章算术》、……、《缀术》等,它们曾经是隋唐时期国子监算学科的教科书.某中学图书馆全部收藏了这10部著作,其中4部是古汉语本,6部是现代译本,若某学生要从中选择2部作为课外读物,至少有一部是现代译本的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥S﹣ABCD的底面为矩形,SA⊥底面ABCD,点E在线段BC上,以AD为直径的圆过点 E.若SA=![]() AB=3,则△SED面积的最小值为_____.
AB=3,则△SED面积的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在极坐标系下,已知圆O:![]() 和直线
和直线![]()
(1)求圆O和直线l的直角坐标方程;
(2)当![]() 时,求直线l与圆O公共点的一个极坐标.
时,求直线l与圆O公共点的一个极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AD=2.
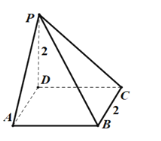
(1)求该四棱锥P-ABCD的表面积和体积;
(2)求该四棱锥P-ABCD内切球的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市拟在长为8 km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数![]() ,
,![]() 的图象,且图象的最高点为
的图象,且图象的最高点为![]() ;赛道的后一部分为折线段MNP.为保证参赛运动员的安全,限定
;赛道的后一部分为折线段MNP.为保证参赛运动员的安全,限定![]() .
.
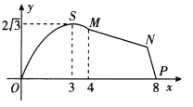
(1)求点M的坐标;
(2)应如何设计,才能使折线段赛道MNP最长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com