
【题目】已知学生的总成绩与数学成绩之间有线性相关关系,下表给出了5名同学在一次考试中的总成绩和数学成绩(单位:分).
学生编号 成绩 | 1 | 2 | 3 | 4 | 5 |
总成绩/x | 482 | 383 | 421 | 364 | 362 |
数学成绩/y | 78 | 65 | 71 | 64 | 61 |
(1)求数学成绩与总成绩的回归直线方程.
(2)根据以上信息,如果一个学生的总成绩为450分,试估计这个学生的数学成绩;
(3)如果另一位学生的数学成绩为92分,试估计其总成绩是多少?
【答案】(1)![]() =14.683+0.132x;(2)大约为74分;(3)586分左右.
=14.683+0.132x;(2)大约为74分;(3)586分左右.
【解析】试题分析:(1)先根据题设条件列表,根据表中数据分别求得![]() ,
,![]() ,由最小二乘法求得
,由最小二乘法求得![]() ,
,![]() ,即可求得回归直线方程;(2)将
,即可求得回归直线方程;(2)将![]() 代入回归直线方程,求得
代入回归直线方程,求得![]() ,即可估计这个学生数学成绩;(3)将
,即可估计这个学生数学成绩;(3)将![]() =92代入回归直线方程,求得
=92代入回归直线方程,求得![]() ,即可估计其总成绩.
,即可估计其总成绩.
试题解析:(1)列出下表,并进行有关计算.
编号 | x | y | x2 | xy |
1 | 482 | 78 | 232 324 | 37 596 |
2 | 383 | 65 | 146 689 | 24 895 |
3 | 421 | 71 | 177 241 | 29 891 |
4 | 364 | 64 | 132 496 | 23 296 |
5 | 362 | 61 | 131 044 | 22 082 |
合计 | 2 012 | 339 | 819 794 | 137 760 |
由上表可得![]() ,
,
可得 ≈0.132,
≈0.132,![]() -0.132×
-0.132×![]() ≈14.683.
≈14.683.
故数学成绩y对总成绩x的回归直线方程为![]() =14.683+0.132x.
=14.683+0.132x.
(2)由(1)得当总成绩x为450分时,![]() =14.683+0.132×450≈74(分),即数学成绩大约为74分.
=14.683+0.132×450≈74(分),即数学成绩大约为74分.
(3)若数学成绩为92分,将![]() =92代入回归直线方程
=92代入回归直线方程![]() =14.683+0.132x中,得x≈586(分).故估计该生的总成绩在586分左右.
=14.683+0.132x中,得x≈586(分).故估计该生的总成绩在586分左右.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】某个体服装店经营某种服装,在某周内获得的纯利润y(单位:元)与该周每天销售这种服装的件数x之间的一组数据关系如下表:
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求纯利润y与每天销售件数x之间的回归方程;
(2)若该周内某天销售服装20件,估计可获得纯利润多少元?
已知:![]() =280,
=280,![]() xiyi=3 487,
xiyi=3 487,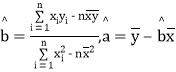 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=sin(4x﹣ ![]() )的图象,只需将函数y=sin4x的图象( )
)的图象,只需将函数y=sin4x的图象( )
A.向左平移 ![]() 单位
单位
B.向右平移 ![]() 单位
单位
C.向左平移 ![]() 单位
单位
D.向右平移 ![]() 单位
单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m6x﹣4x , m∈R.
(1)当m= ![]() 时,求满足f(x+1)>f(x)的实数x的范围;
时,求满足f(x+1)>f(x)的实数x的范围;
(2)若f(x)≤9x对任意的x∈R恒成立,求实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x/元 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y/件 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求线性回归方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =-20,
=-20, ![]() =
=![]() -
-![]()
![]() .
.
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:﹣x2+4x+12≥0,q:x2﹣2x+1﹣m2≤0(m>0).
(Ⅰ)若p是q充分不必要条件,求实数m的取值范围;
(Ⅱ)若“¬p”是“¬q”的充分条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线y2=2px(p>0)的焦点为F,已知点A,B为抛物线上的两个动点,且满足∠AFB=120°.过弦AB的中点M作抛物线准线的垂线MN,垂足为N,则 ![]() 的最大值为 .
的最大值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com