
����Ŀ����֪����y��f1��x����y��f2��x�������庯��f��x��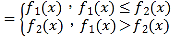 ��
��
��1���躯��f1��x����x+3��f2��x����x2��x������y��f��x���Ľ���ʽ��
��2���ڣ�1���������£�g��x����mx+2��m��R��������h��x����f��x����g��x����������ͬ����㣬��ʵ��m��ȡֵ��Χ��
��3���躯��f1��x����x2��2��f2��x����|x��a|������F��x����f1��x��+f2��x��������F��x������Сֵ��
���𰸡���1��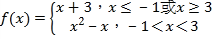 ����2��
����2��![]() ����3��
����3��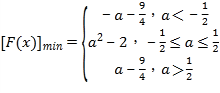
��������
��1�����ݺ���f��x��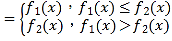 �Ķ��壬����������ȡС��.
�Ķ��壬����������ȡС��.
��2������h��x����f��x����g��x����������ͬ����㣬������f��x����g��x����������ͬ��ʵ��������Ϊ����![]() �Ƿֶκ������������ۣ��ֱ���һ�η��̺Ͷ��η������.
�Ƿֶκ������������ۣ��ֱ���һ�η��̺Ͷ��η������.
��3����������F��x��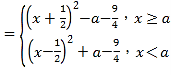 �����ն��κ������������䶯�����ͣ����۶Գ���������˵�ֵ��Ĺ�ϵ����ֵ.
�����ն��κ������������䶯�����ͣ����۶Գ���������˵�ֵ��Ĺ�ϵ����ֵ.
��1����f1��x����x+3��![]() ��
��
��f1��x����f2��x������x��3��x����1ʱ��f��x����x+3��
��f1��x����f2��x��������1��x��3ʱ��![]() ��
��
���ϣ�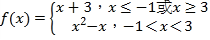 ��
��
��2������h��x����f��x����g��x����������ͬ����㣬
������f��x����g��x����������ͬ��ʵ������
������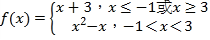 ������g��x����mx+2��m��R����
������g��x����mx+2��m��R����
���Ե�x����1��x��3ʱ��mx+2��x+3ǡ��һ��ʵ���⣬
����![]() ��
��![]() ��
��
��ã�![]() ��
��
����1��x��3ʱ��mx+2��x2��xǡ��������ͬ��ʵ���⣬
������1��x��3ʱx2����m+1��x��2=0ǡ��������ͬ��ʵ���⣬
�躯��h��x����x2����m+1��x��2��
������ɵ�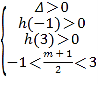 ��
��
����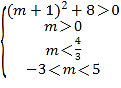 ��
��
���![]() ��
��
���ϣ�m��ȡֵ��ΧΪ![]() ��
��
��3��F��x����f1��x��+f2��x����x2+|x��a|��2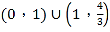 ��
��
����a![]() ������F��x����
������F��x����![]() ���ǵ�������������
���ǵ�������������![]() ���ǵ�����������
���ǵ�����������
��ʱ������F��x������СֵΪ![]() ��
��
����![]() ������F��x���ڣ�������a�����ǵ������������ڣ�a��+�������ǵ�����������
������F��x���ڣ�������a�����ǵ������������ڣ�a��+�������ǵ�����������
��ʱ������F��x������СֵΪF��a����a2��2��
����![]() ������F��x����
������F��x����![]() ���ǵ�������������
���ǵ�������������![]() ���ǵ�����������
���ǵ�����������
��ʱ������F��x������СֵΪ![]() ��
��
���ϣ�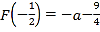 ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() Ϊ��Ȼ�����ĵ�����
Ϊ��Ȼ�����ĵ�����![]() ��.
��.
��1������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2������������![]() ������
������![]() ��ʹ��
��ʹ��![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ���������
���������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ų�Ϊ12����Ϊ8����ƤΧ��Բ���εIJ��棬�����Բ�������Ϊ_____���뾶ΪR�İ�Բ����Ƥ����һ��ԲͲ����ô���ԲͲ�ĸ���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c����![]() ��
��
��1�����A��
��2������ABC���Բ�����Ϊ4�����ҡ�ABC�����![]() �����ABC���ܳ���
�����ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ش�������������, ���������ӻ�֤��.
(1)������������![]() , ��ƽ�����Ƿ���
, ��ƽ�����Ƿ���![]() ������ͬһ��ֱ���ϵĵ�, ʹ�����������ľ��붼Ϊ������?
������ͬһ��ֱ���ϵĵ�, ʹ�����������ľ��붼Ϊ������?
(2)��ƽ�����Ƿ����������ͬ����������ɵĵ㼯![]() , ʹ��
, ʹ��![]() �����е㲻��ͬһ��ֱ����, ��
�����е㲻��ͬһ��ֱ����, ��![]() �����������ľ���Ϊ������?
�����������ľ���Ϊ������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() �������Գ����ľ���Ϊ
�������Գ����ľ���Ϊ![]() ������
������![]() ��ͼ��������ƽ��
��ͼ��������ƽ��![]() ����λ��������ƽ��1����λ�����õĺ���
����λ��������ƽ��1����λ�����õĺ���![]() Ϊ�溯��.
Ϊ�溯��.
��1����![]() �Ľ���ʽ������
�Ľ���ʽ������![]() �ĶԳ����ģ�
�ĶԳ����ģ�
��2��������![]() �ķ���
�ķ���![]() ������
������![]() ������������ȵ�ʵ������ʵ��
������������ȵ�ʵ������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �У�
�� ![]() ��
�� ![]() ƽ��
ƽ��![]() ������
������![]() ����������
����������![]() ��
Ϊ��![]() ���е㣬��
���е㣬��![]() ��
��![]() �ֱ�����
�ֱ�����![]() ��
��![]() �ϣ���
�ϣ���![]() ��
�� ![]() ��
��
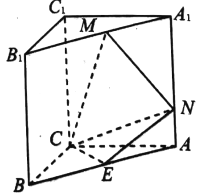
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��������
��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
![]() ��
��![]() ��
��![]() ����֤������
����֤������![]() ʱ��
ʱ��![]() ��
��
![]() ��������
��������![]() ��
��![]() ����������ֵ��
����������ֵ��![]() ��
��![]()
![]() ����bӦ�����������
����bӦ�����������
![]() ��
��![]() ʱ��֤����
ʱ��֤����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵĺ���![]() ���㣺��1��
���㣺��1��![]() ����2��
����2��![]() ����3��
����3��![]() ʱ��
ʱ��![]() .��
.��![]() ��С��ϵ
��С��ϵ
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com