
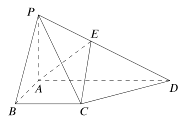
【题目】如图,在四棱锥 ![]() 中,底面
中,底面 ![]() 为直角梯形,
为直角梯形, ![]() ,且
,且 ![]() ,
, ![]() 平面
平面 ![]() .
.
(1)求 ![]() 与平面
与平面 ![]() 所成角的正弦值;
所成角的正弦值;
(2)棱 ![]() 上是否存在一点
上是否存在一点 ![]() 满足
满足 ![]() ?若存在,求
?若存在,求 ![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+x)+mln(1-x)是偶函数,则( )
A.m=1,且f(x)在(0,1)上是增函数
B.m=1,且f(x)在(0,1)上是减函数
C.m=-1,且f(x)在(0,1)上是增函数
D.m=-1,且f(x)在(0,1)上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市收集并整理了该市2017年1月份至10月份各月最低气温与最高气温(单位; ![]() )的数据,绘制了下面的折线图。
)的数据,绘制了下面的折线图。
已知该市的各月最低气温与最高气温具有较好的线性关系,则根据该折线图,下列结论错误的是( )
A.最低气温与最高气温为正相关
B.10月的最高气温不低于5月的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月
D.最低气温低于 ![]() 的月份有4个
的月份有4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺 .问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”.这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一”. 就是说:圆堡瑽(圆柱体)的体积为 ![]() (底面圆的周长的平方
(底面圆的周长的平方 ![]() 高),则由此可推得圆周率
高),则由此可推得圆周率 ![]() 的取值为( )
的取值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线 ![]() 的极坐标方程为
的极坐标方程为 ![]() ,曲线
,曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)设 ![]() 为参数,若
为参数,若 ![]() ,求直线
,求直线 ![]() 的参数方程;
的参数方程;
(2)已知直线 ![]() 与曲线
与曲线 ![]() 交于
交于 ![]() ,设
,设 ![]() ,且
,且 ![]() ,求实数
,求实数 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com