
分析 (1)求出圆的标准方程,即可得到圆心与半径.
(2)设出割线的方程,利用圆心距与半径半弦长的关系,求解斜率,得到直线方程.
解答 解:(1)圆x2+y2-4x+2y-3=0化为标准方程为:(x-2)2+(y+1)2=8,
圆心为P(2,-1),半径r=2$\sqrt{2}$.(4分)
(2)①若割线斜率存在,设AB:y+8=k(x-4),即kx-y-4k-8=0.
设AB的中点为N,则|PN|=$\frac{|2k+1-4k-8|}{\sqrt{k2+1}}$=$\frac{|2k+7|}{\sqrt{k2+1}}$,
由|PN|2+$\frac{{{{|{AB}|}^2}}}{2}$=r2,得k=-$\frac{45}{28}$,
此时AB的直线方程为45x+28y+44=0.(7分)
②若割线斜率不存在,AB:x=4,代入圆方程得y2+2y-3=0,
解得y1=1,y2=-3,符合题意. (10分)
综上,直线AB的方程为45x+28y+44=0或x=4.(12分)
点评 本题考查直线与圆的位置关系的应用,割线方程的求法,考查计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
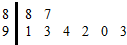 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91 5.5 | B. | 91 5 | C. | 92 5.5 | D. | 92 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②④ | B. | ①③ | C. | ①④ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com