
【题目】在△ABC中,角A、B、C的对边分别为a、b、c.已知cosC=![]() .
.
(1)若![]() ,求△ABC的面积;
,求△ABC的面积;
(2)设向量![]() ,
,![]() ,且
,且![]() ,求sin(B-A)的值.
,求sin(B-A)的值.
【答案】(1)3;(2)![]() .
.
【解析】试题分析:(1)先由数量积求出∠ABC的余弦,进而求出正弦,再利用面积公式求面积;(2)先由向量共线求出∠B,从而得到A,C的关系,再消去A,利用已知条件求值;
试题解析:(1)由![]() ,得abcosC=
,得abcosC=![]() .
.
又因为cosC=![]() ,所以ab=
,所以ab=![]() =
=![]() .又C为△ABC的内角,所以sinC=
.又C为△ABC的内角,所以sinC=![]() .所以△ABC的面积S=
.所以△ABC的面积S=![]() absinC=3.
absinC=3.
(2)因为x//y,所以2sin![]() cos
cos![]() =
=![]() cosB,即sinB=
cosB,即sinB=![]() cosB.
cosB.
因为cosB≠0,所以tanB=![]() .
.
因为B为三角形的内角,所以B=![]() .
.
所以A+C=![]() ,所以A=
,所以A=![]() -C.
-C.
所以sin(B-A)=sin(![]() -A)=sin(C-
-A)=sin(C-![]() )=
)=![]() sinC-
sinC-![]() cosC=
cosC=![]() ×
×![]() -
-![]() ×
×![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣3,3].
(Ⅰ)解不等式:f(x)+f(x+2)>0;
(Ⅱ)若a,b,c均为正实数,且满足a+b+c=m,求证: ![]() +
+ ![]() +
+ ![]() ≥3.
≥3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)=0.5x2﹣bx,(b为常数).
(1)函数f(x)的图象在点(1,f(1))处的切线与函数g(x)的图象相切,求实数b的值;
(2)若函数h(x)=f(x)+g(x)在定义域上不单调,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图①是某市有关部门根据对当地干部的月收入情况调查后画出的样本频率分布直方图,已知图中从左向右第一组的频数为4 000.在样本中记月收入(单位:元)在[1 000,1 500),[1 500,2 000),[2 000,2 500),[2 500,3 000),[3 000,3 500),[3 500,4 000)的人数依次为A1,A2,…,A6.图②是统计月工资收入在一定范围内的人数的算法流程图,则样本的容量n=_____,输出的S=_____.(用数字作答)
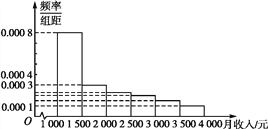
图①
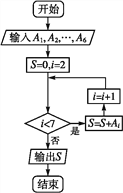
图②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+c,x∈[﹣2,2]表示的曲线过原点,且在x=±1处的切线斜率均为﹣1,给出以下结论: ①f(x)的解析式为f(x)=x3﹣4x,x∈[﹣2,2];
②f(x)的极值点有且仅有一个;
③f(x)的最大值与最小值之和等于0.
其中正确的结论有( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=a(x﹣5)2+6lnx,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为2,4,4.现从这10人中随机选出2人作为该组代表参加座谈会. (I)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率;
(II)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com